题目内容
已知abc≠0, ,一次函数y=kx+k2-2k+2图象上两点为P1(xl,y1),P2 (x2,y2)且|x1-x2|=2,则|P1P2|= .
,一次函数y=kx+k2-2k+2图象上两点为P1(xl,y1),P2 (x2,y2)且|x1-x2|=2,则|P1P2|= .
【答案】分析:根据比例的性质求得k值,然后将其代入一次函数的解析式求得该函数的解析式;最后由一次函数图象上点的坐标特征,求得|y1-y2|=2后,利用两点间的距离公式来求|P1P2|的值.
解答:解:∵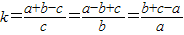 ,
,
∴a+b-c=kc,①
a-b+c=kb,②
b+c-a=ka,③
由①+②+③,得
(a+b+c)=k(a+b+c),
(1)当a+b+c≠0,时,k=1;
∴y=kx+k2-2k+2=x+1,即y=x+1;
又∵一次函数y=kx+k2-2k+2图象上两点为P1(xl,y1),P2 (x2,y2)且|x1-x2|=2,
∴|y1-y2|=2,
∴|P1P2|=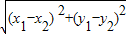 =
=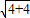 =2
=2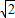 ;
;
(2)当a+b+c=0时,a+b=-c,
则由①式,得
-2c=kc,
∵abc≠0,
∴c≠0,
∴k=-2;
y=kx+k2-2k+2=-2x+10,即y=-2x+10;
又∵一次函数y=kx+k2-2k+2图象上两点为P1(xl,y1),P2 (x2,y2)且|x1-x2|=2,
∴|y1-y2|=4,
∴|P1P2|=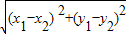 =
=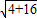 =2
=2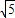 .
.
故答案是:2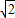 或2
或2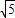 .
.
点评:本题考查了比例的性质、一次函数图象上点的坐标特征.记得在求k值时要分类讨论,以防漏解.
解答:解:∵
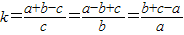 ,
,∴a+b-c=kc,①
a-b+c=kb,②
b+c-a=ka,③
由①+②+③,得
(a+b+c)=k(a+b+c),
(1)当a+b+c≠0,时,k=1;
∴y=kx+k2-2k+2=x+1,即y=x+1;
又∵一次函数y=kx+k2-2k+2图象上两点为P1(xl,y1),P2 (x2,y2)且|x1-x2|=2,
∴|y1-y2|=2,
∴|P1P2|=
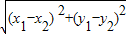 =
=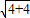 =2
=2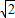 ;
;(2)当a+b+c=0时,a+b=-c,
则由①式,得
-2c=kc,
∵abc≠0,
∴c≠0,
∴k=-2;
y=kx+k2-2k+2=-2x+10,即y=-2x+10;
又∵一次函数y=kx+k2-2k+2图象上两点为P1(xl,y1),P2 (x2,y2)且|x1-x2|=2,
∴|y1-y2|=4,
∴|P1P2|=
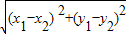 =
=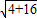 =2
=2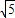 .
.故答案是:2
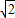 或2
或2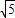 .
.点评:本题考查了比例的性质、一次函数图象上点的坐标特征.记得在求k值时要分类讨论,以防漏解.

练习册系列答案
相关题目
 23、如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上.
23、如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上.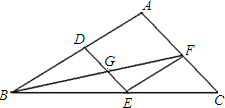 如图,已知△ABC中,有一内接菱形ADEF,连接BF交DE于G点,AB=6,AC=4,
如图,已知△ABC中,有一内接菱形ADEF,连接BF交DE于G点,AB=6,AC=4, 如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上.
如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上. 如图,已知△ABC中,有一内接菱形ADEF,连接BF交DE于G点,AB=6,AC=4,
如图,已知△ABC中,有一内接菱形ADEF,连接BF交DE于G点,AB=6,AC=4,