题目内容
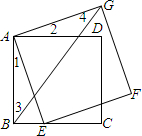 (2013•台湾)如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?( )
(2013•台湾)如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?( )分析:根据正方形的每一个角都是直角求出∠BAD=∠EAG=90°,然后根据同角的余角相等可得∠1=∠2,根据直角三角形斜边大于直角边可得AE>AB,从而得到AG>AB,再根据三角形中长边所对的角大于短边所对的角求出∠3>∠4.
解答:解:∵四边形ABCD、AEFG均为正方形,
∴∠BAD=∠EAG=90°,
∵∠BAD=∠1+∠DAE=90°,
∠EAG=∠2+∠DAE=90°,
∴∠1=∠2,
在Rt△ABE中,AE>AB,
∵四边形AEFG是正方形,
∴AE=AG,
∴AG>AB,
∴∠3>∠4.
故选D.
∴∠BAD=∠EAG=90°,
∵∠BAD=∠1+∠DAE=90°,
∠EAG=∠2+∠DAE=90°,
∴∠1=∠2,
在Rt△ABE中,AE>AB,
∵四边形AEFG是正方形,
∴AE=AG,
∴AG>AB,
∴∠3>∠4.
故选D.
点评:本题考查了正方形的四条边都相等,每一个角都是直角的性质,同角的余角相等的性质,要注意在同一个三角形中,较长的边所对的角大于较短的边所对的角的应用.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
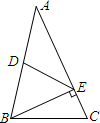 (2013•台湾)如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为何?( )
(2013•台湾)如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为何?( )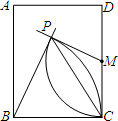 (2013•台湾)如图,长方形ABCD中,M为CD中点,今以B、M为圆心,分别以BC长、MC长为半径画弧,两弧相交于P点.若∠PBC=70°,则∠MPC的度数为何?( )
(2013•台湾)如图,长方形ABCD中,M为CD中点,今以B、M为圆心,分别以BC长、MC长为半径画弧,两弧相交于P点.若∠PBC=70°,则∠MPC的度数为何?( )
 (2013•台湾)如图,
(2013•台湾)如图,