题目内容
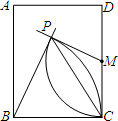 (2013•台湾)如图,长方形ABCD中,M为CD中点,今以B、M为圆心,分别以BC长、MC长为半径画弧,两弧相交于P点.若∠PBC=70°,则∠MPC的度数为何?( )
(2013•台湾)如图,长方形ABCD中,M为CD中点,今以B、M为圆心,分别以BC长、MC长为半径画弧,两弧相交于P点.若∠PBC=70°,则∠MPC的度数为何?( )分析:根据等腰三角形两底角相等求出∠BCP,然后求出∠MCP,再根据等边对等角求解即可.
解答:解:∵以B、M为圆心,分别以BC长、MC长为半径的两弧相交于P点,
∴BP=PC,MP=MC,
∵∠PBC=70°,
∴∠BCP=
(180°-∠PBC)=
(180°-70°)=55°,
在长方形ABCD中,∠BCD=90°,
∴∠MCP=90°-∠BCP=90°-55°=35°,
∴∠MPC=∠MCP=35°.
故选B.
∴BP=PC,MP=MC,
∵∠PBC=70°,
∴∠BCP=
| 1 |
| 2 |
| 1 |
| 2 |
在长方形ABCD中,∠BCD=90°,
∴∠MCP=90°-∠BCP=90°-55°=35°,
∴∠MPC=∠MCP=35°.
故选B.
点评:本题考查了矩形的四个角都是直角的性质,等腰三角形两底角相等的性质以及等边对等角,是基础题.

练习册系列答案
相关题目
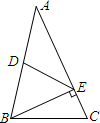 (2013•台湾)如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为何?( )
(2013•台湾)如图,△ABC中,D为AB中点,E在AC上,且BE⊥AC.若DE=10,AE=16,则BE的长度为何?( )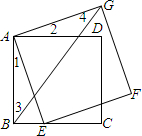 (2013•台湾)如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?( )
(2013•台湾)如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?( )
 (2013•台湾)如图,
(2013•台湾)如图,