��Ŀ����
����Ŀ����ͼ���ڱ�ֱ�ĺ�����l����A��B�����۲�վ��A��B����������AB=��![]() +1��km��С���ڵ�P������A���С���ڱ�ƫ��60��ķ���B���С���ڱ�ƫ��45�㷽��
+1��km��С���ڵ�P������A���С���ڱ�ƫ��60��ķ���B���С���ڱ�ƫ��45�㷽��
��1�����P��������l�ľ��룻
��2��С���ӵ�P��������AP�ķ�����һ��ʱ������C������ʱ����B���С���ڱ�ƫ��15��ķ������C���B֮��ľ��룮��������ʾ��������������ţ�
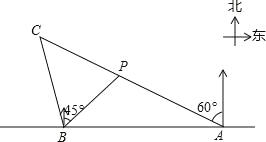
���𰸡���1����P��������l�ľ���Ϊ1km����2����C���B֮��ľ���Ϊ![]() km��
km��
��������
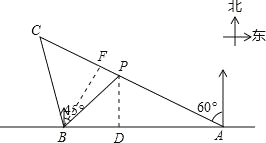
�����������1����ͼ������P��PD��AB�ڵ�D����PD=xkm��
��Rt��PBD�У���BDP=90�㣬��PBD=90��-45��=45�㣬
��BD=PD=xkm��
��Rt��PAD�У���ADP=90�㣬��PAD=90��-60��=30�㣬
��AD=![]() PD=
PD=![]() xkm��
xkm��
��BD+AD=AB��
��x+![]() x=
x=![]() +1��
+1��
x=1��
����P��������l�ľ���Ϊ1km��
��2����ͼ������B��BF��AC�ڵ�F��
��������ã���ABC=105�㣬
��Rt��ABF�У���AFB=90�㣬��BAF=30�㣬
��BF=![]() AB=
AB=![]() km��
km��
����ABC�У���C=180��-��BAC-��ABC=45�㣮
��Rt��BCF�У���BFC=90�㣬��C=45�㣬
��BC=![]() BF=
BF=![]() km��
km��
����C���B֮��ľ���Ϊ![]() km��
km��

��ϰ��ϵ�д�
�����Ŀ