题目内容
如图，某农户想利用自家院子一面墙和20米长的篱笆围成一个矩形养鸡场，并留出一个1米宽的口子用来进出．
（1）若围成的养鸡场面积为54m2，求围成的养鸡场的长和宽；
（2）请用配方法，求出能围成的矩形养鸡场的最大面积，并说明设计方案．
解：（1）设养鸡场的宽为xm，则长为（50-2x）m，由题意列方程得，
x（21-2x）=54，
解得x1=6，x2=4.5；
当x1=6时，21-2x=9；
当x2=4.5时，21-2x=12；
答：长方形养鸡场的长和宽分别为6米，9米或4.5米，12米．
（2）设矩形场地的面积为S，
则S=x（21-x）=-2（x-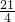
）2+
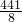
∴当x=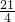时，面积最大值为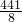米．
分析：（1）设长方形的养鸡场的宽为xm，则长为（21-2x）m，由题意列方程即可解答；
（2）利用配方法确定最大值即可．
点评：本题考查了一元二次方程的应用，根据长方形的面积公式，也可利用枚举法，得出如何围才能够使面积最大．
x（21-2x）=54，
解得x1=6，x2=4.5；
当x1=6时，21-2x=9；
当x2=4.5时，21-2x=12；
答：长方形养鸡场的长和宽分别为6米，9米或4.5米，12米．
（2）设矩形场地的面积为S，
则S=x（21-x）=-2（x-
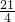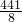
）2+∴当x=
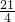时，面积最大值为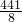米．分析：（1）设长方形的养鸡场的宽为xm，则长为（21-2x）m，由题意列方程即可解答；
（2）利用配方法确定最大值即可．
点评：本题考查了一元二次方程的应用，根据长方形的面积公式，也可利用枚举法，得出如何围才能够使面积最大．
练习册系列答案
通城学典默写能手系列答案
相关题目
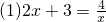；（2）7x=9；（3）4x-2=3x+1；（4）x2+6x+9=0；（5）x=3；（6）x+y=8．其中是一元一次方程的个数是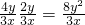
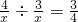
如图，已知等腰△ABC，AB=AC，过A、C两点的圆⊙O切AB于A，BC的延长线交⊙O于D，∠ABD的角平分线交AC于E，交AD于F．