题目内容
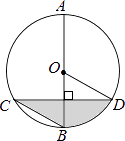
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,求
,求![]() 的长度.
的长度.

【答案】(1)∠CFD=63°;(2)AD=![]()
【解析】
(1)根据三角形的内角和以及平行线的性质解答即可;
(2)勾股定理求出AC的长度,根据角平分线的性质得到DC=DE,证明Rt△BED≌Rt△BCD(HL),得到BE=BC=5,从而得出AE=8,设DE=DC=x,则AD=12-x,在Rt△ADE中利用勾股定理,列出方程解出x,即可求出AD.
解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=36°,
∴∠ABC=90°-36°=54°,
∵BD平分∠ABC交AC于点D,
∴∠ABD=∠DBC=27°,
∴∠BDC=63°,
∵DE⊥AB,
∴∠ADE=90°-36°=54°,
∵CF∥BD,
∴∠DCF=∠BDC=63°.
∵∠CDF=∠ADE=54°,
∴∠CFD=180°∠DCF∠CDF=63°.
(2)∵在Rt△ABC中,AB=13,BC=5,
∴AC=![]() ,
,
∵BD平分∠ABC,∠C=90°,DE⊥AB,
∴DC=DE,
在Rt△BED与Rt△BCD中,
DE=DC,BD=BD,
∴Rt△BED≌Rt△BCD(HL)
∴BE=BC=5,
∴AE=13-5=8,
设DE=DC=x,
则AD=12-x,
在Rt△ADE中,AE2+DE2=AD2,即82+x2=(12-x)2,解得:x=![]() ,
,
∴AD=12-![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层。第二层……第n层,第n层的小正方体的个数记为S.解答下列问题:
(1)填写表格:
n | 1 | 2 | 3 | 4 | … |
S | 1 |
| … |
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?