题目内容
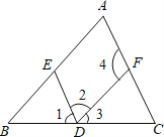
【题目】如图，CD是线段AB的垂直平分线，则∠CAD=∠CBD.请说明理由：
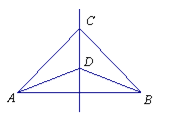
解：∵ CD是线段AB的垂直平分线
∴ AC=BC,AD=DB（ ）
在△ADC和△BDC中，
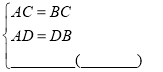
∴△ADC≌和△BDC( ）.
∴ ∠CAD=∠CBD（ ）.
【答案】垂直平分线定理，CD=CD，公共边，SSS，全等三角形对应角相等.
【解析】
根据线段垂直平分线性质得出AC=BC，AD=BD，根据SSS证出△ACD≌△BCD即可．
解：∵CD是线段AB的垂直平分线，
∴AC=BC，AD=BD，（垂直平分线定理）
在△ADC和△BDC中，
∴△ADC≌和△BDC( SSS）.
∴ ∠CAD=∠CBD（全等三角形对应角相等）.
故答案为：垂直平分线定理，CD=CD，公共边，SSS，全等三角形对应角相等.
练习册系列答案
智慧小复习系列答案
相关题目
