题目内容
【题目】如图甲,AB⊥BD,CD⊥BD,AP⊥PC,垂足分别为B、P、D,且三个垂足在同一直线上,我们把这样的图形叫“三垂图”.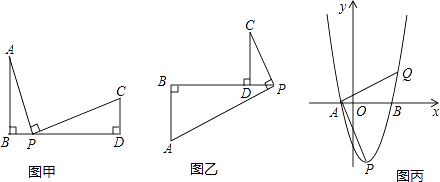
(1)证明:ABCD=PBPD.
(2)如图乙,也是一个“三垂图”,上述结论成立吗?请说明理由.
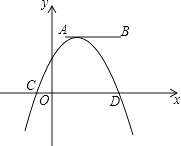
(3)已知抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点(0,﹣3),顶点为P,如图丙所示,若Q是抛物线上异于A、B、P的点,使得∠QAP=90°,求Q点坐标.
【答案】
(1)
证明:∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴∠A+∠APB=90°,
∵AP⊥PC,
∴∠APB+∠CPD=90°,
∴∠A=∠CPD,
∴△ABP∽△PCD,
∴ ![]() =
= ![]() ,
,
∴ABCD=PBPD
(2)
ABCD=PBPD仍然成立.
理由如下:∵AB⊥BD,CD⊥BD,
∴∠B=∠CDP=90°,
∴∠A+∠APB=90°,
∵AP⊥PC,
∴∠APB+∠CPD=90°,
∴∠A=∠CPD,
∴△ABP∽△PCD,
∴ ![]() =
= ![]() ,
,
∴ABCD=PBPD
(3)
设抛物线解析式为y=ax2+bx+c(a≠0),
∵抛物线与x轴交于点A(﹣1,0),B(3,0),与y轴交于点(0,﹣3),
∴ 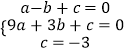 ,
,
解得 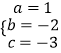 ,
,
所以,y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点P的坐标为(1,﹣4),
过点P作PC⊥x轴于C,设AQ与y轴相交于D,

则AO=1,AC=1+1=2,PC=4,
根据(2)的结论,AOAC=ODPC,
∴1×2=OD4,
解得OD= ![]() ,
,
∴点D的坐标为(0, ![]() ),
),
设直线AD的解析式为y=kx+b(k≠0),
则 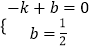 ,
,
解得 ![]() ,
,
所以,y= ![]() x+
x+ ![]() ,
,
联立 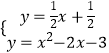 ,
,
解得 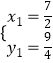 ,
, ![]() (为点A坐标,舍去),
(为点A坐标,舍去),
所以,点Q的坐标为( ![]() ,
, ![]() ).
).
【解析】(1)根据同角的余角相等求出∠A=∠CPD,然后求出△ABP和△PCD相似,再根据相似三角形对应边成比例列式整理即可得证;(2)与(1)的证明思路相同;(3)利用待定系数法求出二次函数解析式,根据抛物线解析式求出点P的坐标,再过点P作PC⊥x轴于C,设AQ与y轴相交于D,然后求出PC、AC的长,再根据(2)的结论求出OD的长,从而得到点D的坐标,利用待定系数法求出直线AD的解析式,与抛物线解析式联立求解即可得到点Q的坐标.