题目内容
【题目】 ⑴如图![]() ,在正方形
,在正方形![]() 中,点
中,点![]() 分别在
分别在![]() 上,
上,![]() 于点
于点![]() ,求证
,求证![]() ;
;
⑵如图![]() ,将⑴中的正方形
,将⑴中的正方形![]() 改为矩形
改为矩形![]() ,
,![]()
![]() 于点
于点![]() ,探究
,探究![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.

【答案】(1)见解析;(2)AB=![]() BC,见解析.
BC,见解析.
【解析】
试题分析:(1)根据正方形的性质,可得∠ABC与∠C的关系,AB与BC的关系,根据两直线垂直,可得∠AMB的度数,根据直角三角形锐角的关系,可得∠ABM与∠BAM的关系,根据同角的余角相等,可得∠BAM与∠CBF的关系,根据ASA,可得△ABE≌△BCF,根据全等三角形的性质,可得答案;
(2)根据矩形的性质得到∠ABC=∠C,由余角的性质得到∠BAM=∠CBF,根据相似三角形的性质即可得到结论.
试题解析(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠C,AB=BC.
∵AE⊥BF,∴∠AMB=∠BAM+∠ABM=90°,
∵∠ABM+∠CBF=90°,∴∠BAM=∠CBF.
在△ABE和△BCF中,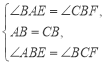 ,
,
∴△ABE≌△BCF(ASA),∴AE=BF;
(2)解:AB=![]() BC,
BC,
理由:∵四边形ABCD是矩形,∴∠ABC=∠C,
∵AE⊥BF,∴∠AMB=∠BAM+∠ABM=90°,
∵∠ABM+∠CBF=90°,∴∠BAM=∠CBF,∴△ABE∽△BCF,
∴![]() ,∴AB=
,∴AB=![]() BC.
BC.

【题目】某中学女子足球队15名队员的年龄情况如下表:
年龄(岁) | 13 | 14 | 15 | 16 |
队员(人) | 2 | 3 | 6 | 4 |
这支球队队员的年龄的众数和中位数分别是( )
A.14,15
B.14,14.5
C.15,15
D.15,14
【题目】 九⑴班![]() 名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下
名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下![]() 名学生成绩尚未统计,这
名学生成绩尚未统计,这![]() 名学生成绩如下:
名学生成绩如下:![]() .
.
频数分布表
分数段 | 频数(人数) |
|
|
|
|
|
|
|
|

请解答下列问题:
⑴完成频数分布表,![]() ,
,![]() .
.
⑵补全频数分布直方图;
⑶全校共有![]() 名学生参加初赛,估计该校成绩
名学生参加初赛,估计该校成绩![]() 范围内的学生有多少人?
范围内的学生有多少人?
⑷九⑴班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
