题目内容
 已知:如图,BD∥AF∥CE,∠ABD=60°,∠ACE=36°,AP是∠BAF的平分线,求∠PAC的度数.
已知:如图,BD∥AF∥CE,∠ABD=60°,∠ACE=36°,AP是∠BAF的平分线,求∠PAC的度数.
解:∵BD∥AF,∠ABD=60°,
∴∠BAF=∠ABD=60°,
∵AP平分∠BAF,
∴∠PAF= ∠BAF=30°,
∠BAF=30°,
又∵AF∥CE,∠ACE=36°,
∴∠CAF=∠ACE=36°.
∴∠PAC=∠PAF+∠CAF=30°+36°=66°.
分析:由BD∥AF,∠ABD=60°,根据两直线平行,内错角相等,即可求得∠BAF的度数,又由AP是∠BAF的平分线,即可求得∠PAF的度数,然后由AF∥CE,∠ACE=36°,根据两直线平行,内错角相等,即可求得∠CAF的度数,继而求得∠PAC的度数.
点评:此题考查了平行线的性质与角平分线的定义.解题的关键是注意掌握两直线平行,内错角相等定理的应用.
∴∠BAF=∠ABD=60°,
∵AP平分∠BAF,
∴∠PAF=
 ∠BAF=30°,
∠BAF=30°,又∵AF∥CE,∠ACE=36°,
∴∠CAF=∠ACE=36°.
∴∠PAC=∠PAF+∠CAF=30°+36°=66°.
分析:由BD∥AF,∠ABD=60°,根据两直线平行,内错角相等,即可求得∠BAF的度数,又由AP是∠BAF的平分线,即可求得∠PAF的度数,然后由AF∥CE,∠ACE=36°,根据两直线平行,内错角相等,即可求得∠CAF的度数,继而求得∠PAC的度数.
点评:此题考查了平行线的性质与角平分线的定义.解题的关键是注意掌握两直线平行,内错角相等定理的应用.

练习册系列答案
相关题目
 已知:如图,BD是AC边上的高,DE⊥BC于E,BE:EC=5:1.若AD=2,AB=8.
已知:如图,BD是AC边上的高,DE⊥BC于E,BE:EC=5:1.若AD=2,AB=8.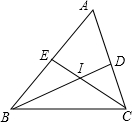 已知:如图,BD平分∠ABC,CE平分∠ACE,BD与CE交于点I,试说明∠BIC=90°+
已知:如图,BD平分∠ABC,CE平分∠ACE,BD与CE交于点I,试说明∠BIC=90°+ 22、已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.
22、已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.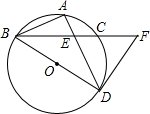 已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连接AB.
已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连接AB. 已知:如图,BD、CE是△ABC的两条高,M是BC的中点.求证:ME=MD.
已知:如图,BD、CE是△ABC的两条高,M是BC的中点.求证:ME=MD.