题目内容
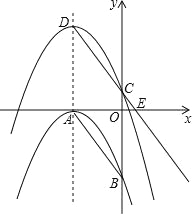
【题目】如图，抛物线C1：y=﹣
（x+3）2与x，y轴分别相交于点A，B，将抛物线C1沿对称轴向上平移，记平移后的抛物线为C2，抛物线C2的顶点是D，与y轴交于点C，射线DC与x轴相交于点E，
（1）求A，B点的坐标；
（2）当CE：CD=1：2时，求此时抛物线C2的顶点坐标；
（3）若四边形ABCD是菱形．
①此时抛物线C2的解析式；
②点F在抛物线C2的对称轴上，且点F在第三象限，点M在抛物线C2上，点P是坐标平面内一点，是否存在以A，F，P，M为顶点的四边形与菱形ABCD相似，并且这个菱形以A为顶点的角是钝角，若存在求出点F的坐标，若不存在请说明理由．
【答案】（1）A（﹣3，0），B（0，﹣4）；（2）（3，2）（3，6）（3）①
②
，
，
【解析】
试题分析：（1）利用坐标轴上点的特点，确定出点A，B的坐标；
（2）根据锐角三角函数的意义，和抛物线的平移，得到比例式，求出即可；
（3）①由点的移动情况判断出抛物线的移动情况；
②设出点的坐标，M（3+3a，4a），表示出F（3，﹣5a）．根据点在抛物线上，求出a，从而得到F的坐标．
试题解析：（1）令y=0，
∴y=﹣
（x+3）2=0，
∴x=3，
令x=0，
∴y=4，
∴A（﹣3，0），B（0，﹣4）；
（2）由（1）得：OA=3，OB=4，
∴tan∠OBA=
．
由题意得AB∥CD，∠EDA=∠OBA，
∴
．
①当点C在y轴负半轴时，
由CE：CD=1：2，
∴OE=EA=1.5，AD=2，
∴D（3，2）；
②当点C在y轴正半轴时，
由CE：CD=1：2，
∴OE：OA=1：2，
∴AE=4.5，
∴AD=6，
∴D（3，6）．
（3）①由解析式可得A（﹣3，0），B（0，﹣4），
∴AB=BC=AD=DC=5，
即抛物线向上平移5个单位，因此抛物线C2
解析式为
；
②I：如图，以AF为边在对称轴右侧作菱形时，延长BA，与抛物线C2 交于点G，
∴∠FAG=∠BAD．
当AF=AM时，点M与点G重合，菱形AMPF∽菱形ABCD，
∵tan∠AMP=tan∠OBA=
∴设M（3+3a，4a），F（3，﹣5a）．
把M点坐标代入
，
可得a1=
﹣1，
（舍去），
．
当AF=AP时，
∴设M（3+3a，﹣a），F（3，﹣5a）．
把M点坐标代入
，
可得a1=﹣1 （舍去），
，
．
以AF为边在对称轴左侧作菱形时，点F坐标不变．
II：以AF为对角线作菱形时，
由菱形的对角线性质可知，
在AF右侧作∠FAP=∠FAM，
∴∠PAF=∠GAF=∠BAD，
菱形的轴对称性可得P点也在抛物线C2 上．
设M（3+3a，﹣a），F（3，﹣2a），
∴，
∴
．
当点M在AF左侧时，F点坐标不变．
当点M在AF左侧时，F点坐标不变．
综上所述：
，
，
