题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,连接
上一点,连接![]()
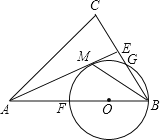
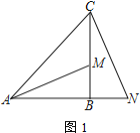
(1)如图1,若![]() ,
,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 与
与![]() 垂直,求证:
垂直,求证:![]()
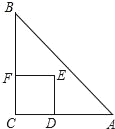
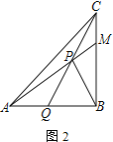
(2)过点![]() 作
作![]() ,
,![]() 为垂足,连接
为垂足,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
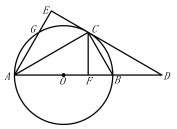
①如图2,若![]() ,求证:
,求证:![]()
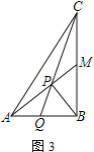
②如图3,若![]() 是
是![]() 的中点,直接写出
的中点,直接写出![]() 的值(用含
的值(用含![]() 的式子表示)
的式子表示)
【答案】(1)证明见解析;(2)①证明见解析;②![]()
【解析】
(1)延长![]() 交
交![]() 于点
于点![]() ,证明
,证明![]() 即可得;
即可得;
(2)①过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,由(1),得
,由(1),得![]() ,再根据平行线分线段成比例定理即可得到结论;
,再根据平行线分线段成比例定理即可得到结论;
②过点C作CD//BP交AB的延长线于点D,延长AM交CD于点H,先证明△BPM≌△CHM,从而可得BP=CH,PM=HM,再证明△ABM∽△BPM,得到![]() ,在Rt△PCH中,由tan∠PCH=
,在Rt△PCH中,由tan∠PCH=![]() 可得tan∠BPQ=
可得tan∠BPQ=![]() ,继而根据BC=2BM,
,继而根据BC=2BM,![]() 即可求得答案.
即可求得答案.
(1)延长![]() 交
交![]() 于点
于点![]() ,
,

∵![]() 与
与![]() 垂直,
垂直,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)①过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,

∵![]() ,∴
,∴![]() 与
与![]() 垂直,
垂直,
由(1),得![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ;
;
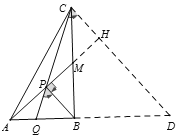
②过点C作CD//BP交AB的延长线于点D,延长AM交CD于点H,
∴∠PCH=∠BPQ,
∵![]() ,∴
,∴![]() ⊥
⊥![]() ,
,
∴∠BPM=∠CHM=90°,
又∵∠BMP=∠CMH,BM=CM,
∴△BPM≌△CHM,
∴BP=CH,PM=HM,
∴PH=2PM,
∵∠PMB=∠BMA,∠ABM=∠BPM=90°,
∴△ABM∽△BPM,
∴![]() ,
,
在Rt△PCH中,tan∠PCH=![]() ,
,
∴tan∠BPQ=![]() ,
,
又∵BC=2BM,![]() ,
,
∴tan∠BPQ=![]() .
.

练习册系列答案
相关题目