题目内容
如图,四边形OABC为直角梯形,OA=10,OC=3,BC=6.动点P、Q分别从C、A两点同时出发,点P以每秒1个单 位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5),
位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5),
(1)当t为多少时,四边形PQAB是平行四边形?
(2)当t为多少时,四边形PQAB是等腰梯形?
 位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5),
位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,当点Q停止运动时,点P也停止运动,设运动时间为t(0≤t≤5),(1)当t为多少时,四边形PQAB是平行四边形?
(2)当t为多少时,四边形PQAB是等腰梯形?
分析:(1)由题意可得CP=t,AQ=2t,BP=BC-CP=6-t,又由当BP=AQ时,四边形PQAB是平行四边形,可得方程6-t=2t,解此方程即可求得t的值;
(2)由当PQ=AB,PB≠AQ时,四边形PQAB是等腰梯形,可得方程:4+6-t+4=2t,解此方程即可求得t的值.
(2)由当PQ=AB,PB≠AQ时,四边形PQAB是等腰梯形,可得方程:4+6-t+4=2t,解此方程即可求得t的值.
解答:解:∵四边形OABC为直角梯形,OA=10,OC=3,BC=6,点P以每秒1个单位的速度由C向B运动,点Q以每秒2个单位的速度由A向O运动,
∴CP=t,AQ=2t,
∴BP=BC-CP=6-t,
(1)∵四边形OABC为直角梯形,
∴BC∥OA,
∴当BP=AQ时,四边形PQAB是平行四边形,
即6-t=2t,
即t=2,
故当t为2时,四边形PQAB是平行四边形;
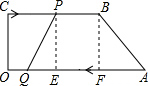 (2)过点P作PE⊥OA于点E,过点B作BF⊥OA于点F,
(2)过点P作PE⊥OA于点E,过点B作BF⊥OA于点F,
∵OA∥BC,
∴四边形PBFE是矩形,四边形OCBF是矩形,
∴EF=BP=6-t,PE=BF,OF=BC,
∴AF=OA-BC=10-6=4,
∵当PQ=AB,PB≠AQ时,四边形PQAB是等腰梯形,
在Rt△PQE和Rt△BAF中,
∵
,
∴Rt△PQE≌Rt△BAF(HL),
∴QE=AF=4,
∵QE+EF+AF=AQ,
∴4+6-t+4=2t,
解得:t=
,
故当t为
时,四边形PQAB是等腰梯形.
∴CP=t,AQ=2t,
∴BP=BC-CP=6-t,
(1)∵四边形OABC为直角梯形,
∴BC∥OA,
∴当BP=AQ时,四边形PQAB是平行四边形,
即6-t=2t,
即t=2,
故当t为2时,四边形PQAB是平行四边形;
 (2)过点P作PE⊥OA于点E,过点B作BF⊥OA于点F,
(2)过点P作PE⊥OA于点E,过点B作BF⊥OA于点F,∵OA∥BC,
∴四边形PBFE是矩形,四边形OCBF是矩形,
∴EF=BP=6-t,PE=BF,OF=BC,
∴AF=OA-BC=10-6=4,
∵当PQ=AB,PB≠AQ时,四边形PQAB是等腰梯形,
在Rt△PQE和Rt△BAF中,
∵
|
∴Rt△PQE≌Rt△BAF(HL),
∴QE=AF=4,
∵QE+EF+AF=AQ,
∴4+6-t+4=2t,
解得:t=
| 14 |
| 3 |
故当t为
| 14 |
| 3 |
点评:此题考查了直角梯形的性质、平行四边形的性质以及等腰梯形的性质.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
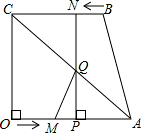 动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.
动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ. 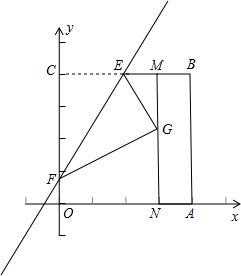 在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.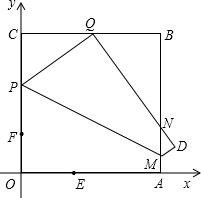
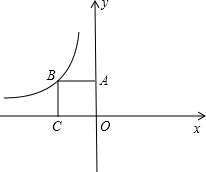 (2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数
(2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数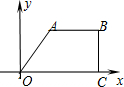 是( )
是( )