题目内容
【题目】抛物线y=x2+4ax+b与x轴相交于O、A两点（其中O为坐标原点），过点P（2，2a）作直线PM⊥x轴于点M，交抛物线于点B，点B关于抛物线对称轴的对称点为C（其中B、C不重合），连接AP交y轴于点N，连接BC和PC．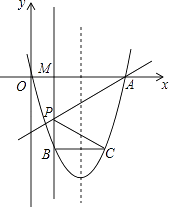 
（1）a= 
时，求抛物线的解析式和BC的长；
（2）如图a＜﹣1时，若AP⊥PC，求a的值．
【答案】
（1）解：当a= 
时，
∴抛物线为：y=x2+6x+b，
∴对称轴为x=﹣3，
又∵抛物线过原点，
∴b=0，
∴y=x2+6x，
∴令x=2代入y=x2+6x，
∴y=16，
∴B（2，16），
∵点B关于抛物线对称轴的对称点为C，
∴C（﹣8，16），
∴BC=2﹣（﹣8）=10
（2）解：由于抛物线过原点O，
∴b=0，
∴y=x2+4ax，
令x=2代入y=x2+4ax，
∴y=4+8a，
∴B（2，4+8a），
∵∵点B关于抛物线对称轴的对称点为C，
抛物线的对称轴为x=﹣2a，
∴C（﹣4a﹣2，4+8a），
∵O与A关于x=﹣2a对称，
∴A（﹣4a，0），
∴BC=﹣4a﹣2﹣2=﹣4a﹣4，
∵P（2，2a），
∴M（2，0），
∴PM=0﹣2a=﹣2a，AM=﹣4a﹣2，
BP=2a﹣（4+8a）=﹣4﹣6a，
∵AP⊥PC，
∴∠APM=∠PCB，
∴△AMP∽△BPC，
∴ 
，
∴ 
= 
，
∴a=﹣2 
，
∵a＜﹣1，
∴a=﹣2﹣ 
【解析】（1）令a= 代入抛物线，由于抛物线过原点，所以b=0，从而求出抛物线的解析式，然后根据条件求出点B与C的坐标即可求出BC的长度．（2）由题意可知b=0，然后根据P的坐标分别求出A、B、C、M的坐标，进而求出BC、BP、PM、AM的长度，最后利用△AMP∽△BPC列出关于a的方程即可求出a的值．
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系和抛物线与坐标轴的交点，掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）；一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．即可以解答此题．
