题目内容
 已知平面直角坐标系内,一次函数y=kx+2的图象与x轴相交于点A(-2
已知平面直角坐标系内,一次函数y=kx+2的图象与x轴相交于点A(-2| 3 |
(1)求一次函数的解析式,并在直角坐标系中画出它的图象;
(2)若以原点O为圆心的⊙O与直线AB相切于点C,求⊙O的半径和点C的坐标;
(3)在x轴上是否存在点P,使△PAB为等腰三角形?若存在,请写出点P的坐标;若不存在,请说明理由.
分析:(1)根据已知条件把点A(-2
,0)代入y=kx+2,解出k的值,即可求出解析式.
(2)先过点O作OC⊥AB,得出它与y轴的交点坐标,再根据正切定义,得出∠OAB的度数,再根据在直角△CAB中,OC、OA的值,即可求出⊙O的半径,再过点C作CD⊥OA于D,得出CD、OD的值,最后得出点C的坐标.
(3)本题需先判断出P的存在,再根据题意得出AB的值,再以A、B为顶角的顶点和以AB为腰时,分别求出P点的坐标.
| 3 |
(2)先过点O作OC⊥AB,得出它与y轴的交点坐标,再根据正切定义,得出∠OAB的度数,再根据在直角△CAB中,OC、OA的值,即可求出⊙O的半径,再过点C作CD⊥OA于D,得出CD、OD的值,最后得出点C的坐标.
(3)本题需先判断出P的存在,再根据题意得出AB的值,再以A、B为顶角的顶点和以AB为腰时,分别求出P点的坐标.
解答: 解:(1)∵一次函数y=kx+2的图象与x轴相交于A,
解:(1)∵一次函数y=kx+2的图象与x轴相交于A,
∴把点A(-2
,0)代入y=kx+2得:
-2
k+2=0,
k=
,
∴一次函数的解析式:y=
x+2;
(2)过点O作OC⊥AB于C,
∵一次函数的解析式:y=
x+2,
∴它与y轴的交点坐标为(0,2),
∴OA=2
,OB=2,
∴tan∠OAB=
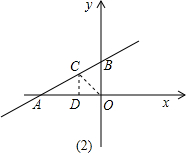
∴∠OAB=30°
∴在Rt△CAB中,OC=
OA=
,
∴⊙O的半径为
,
过点C作CD⊥OA于D,
∴CD=
,OD=
,
∴点C的坐标为(-
,
)
(3)在x轴上存在点P,使△PAB为等腰三角形,
由题意得,AB=4
当以A为顶角的顶点时,P(-4-2
,0),
当以B为顶角的顶点时,P(2
,0),
当以AB为腰时,P(-
,0)
 解:(1)∵一次函数y=kx+2的图象与x轴相交于A,
解:(1)∵一次函数y=kx+2的图象与x轴相交于A,∴把点A(-2
| 3 |
-2
| 3 |
k=
| ||
| 3 |
∴一次函数的解析式:y=
| ||
| 3 |
(2)过点O作OC⊥AB于C,
∵一次函数的解析式:y=
| ||
| 3 |
∴它与y轴的交点坐标为(0,2),
∴OA=2
| 3 |
∴tan∠OAB=
| ||
| 3 |

∴∠OAB=30°
∴在Rt△CAB中,OC=
| 1 |
| 2 |
| 3 |
∴⊙O的半径为
| 3 |
过点C作CD⊥OA于D,
∴CD=
| 3 |
| 2 |
| ||
| 2 |
∴点C的坐标为(-
| ||
| 2 |
| 3 |
| 2 |
(3)在x轴上存在点P,使△PAB为等腰三角形,
由题意得,AB=4
当以A为顶角的顶点时,P(-4-2
| 3 |
当以B为顶角的顶点时,P(2
| 3 |
当以AB为腰时,P(-
2
| ||
| 3 |
点评:本题主要考查了一次函数的综合,在解题时要注意知识的综合应用以及各点的求法是本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
已知平面直角坐标系内点P(4,6),将其向左平移4个单位后得到点Q,那么△POQ的面积为( )

| A、24 | B、12 | C、8 | D、6 |