题目内容
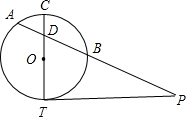如图，PT是⊙O的切线，T为切点，PA是割线，交⊙O于A、B两点，与直径CT交于点D．已知CD=2，AD=3，BD=4，那PB=分析：由相交弦定理得AD•BD=CD•DT，求得TD，由切割线定理得PT2=PA•PB，由勾股定理得PT2=PD2-TD2，则PA•PB=PD2-TD2，从而求得PB．
解答：解：∵AD•BD=CD•DT，
∴TD=
，
∵CD=2，AD=3，BD=4，
∴TD=6，
∵PT是⊙O的切线，PA是割线，
∴PT2=PA•PB，
∵CT为直径，
∴PT2=PD2-TD2，
∴PA•PB=PD2-TD2，
即（PB+7）PB=（PB+4）2-62，
解得PB=20．
故答案为：20．
∴TD=
| AD•BD |
| CD |
∵CD=2，AD=3，BD=4，
∴TD=6，
∵PT是⊙O的切线，PA是割线，
∴PT2=PA•PB，
∵CT为直径，
∴PT2=PD2-TD2，
∴PA•PB=PD2-TD2，
即（PB+7）PB=（PB+4）2-62，
解得PB=20．
故答案为：20．
点评：本题考查了相交弦定理和切割线定理，解此题的关键是熟记相交弦定理和切割线定理的内容，是中档题．
练习册系列答案
相关题目
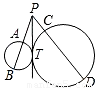
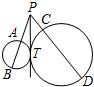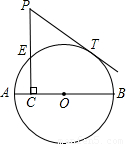
8、如图，PT是外切两圆的公切线，T为切点，PAB，PCD分别为这两圆的割线．若PA=3，PB=6，PC=2，则PD等于（ ）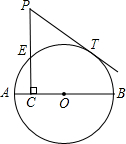
如图，AB是⊙O的直径，点C在⊙O的半径AO上运动，PC⊥AB交⊙O于E，PT切⊙O于T，PC=2.5．
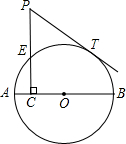如图，AB是⊙O的直径，点C在⊙O的半径AO上运动，PC⊥AB交⊙O于E，PT切⊙O于T，PC=2.5．
