Question

如图，AB是⊙O的直径，点C在⊙O的半径AO上运动，PC⊥AB交⊙O于E，PT切⊙O于T，PC=2.5．
（1）当CE正好是⊙O的半径时，PT=2，求⊙O的半径；
（2）设PT²=y，AC=x，求出y与x之间的函数关系式；
（3）△PTC能不能变为以PC为斜边的等腰直角三角形？若能，请求出△PTC的面积；若不能，请说明理由．

Answer 1

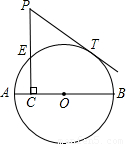
【答案】分析：（1）如图1所示：当CE正好是⊙O的半径时，点C与圆心O重合．连接OT．由切线的性质推知△PCT为直角三角形，所以在Rt△PCT中利用勾股定理即可求得⊙O的半径OT的长度；
（2）连接OP、OT，由在Rt△POT和Rt△PCO中利用勾股定理得PT²+OT²=PC²+OC²，化简得y=x²-3x+6.25（0≤x≤1.5）；
（3）△PTC不可能变为以PC为斜边的等腰直角三角形．当PT⊥CT时，由于PT切⊙O于T，所以CT过圆心，即CT就是⊙O的半径，如图1所示．由（1）知，CT=1.5，PT=2，即PT≠CT，故△PTC不可能变为以PC为斜边的等腰直角三角形．
解答：解：（1）如图1所示：当CE正好是⊙O的半径时，点C与圆心O重合．连接OT．
∵PT切⊙O于T，
∴PT⊥OT，
∴∠PTO=90°．
在Rt△PCT中，PC=2.5，PT=2，
根据勾股定理知，OT==1.5，即⊙O的半径为1.5；

（2）如图2所示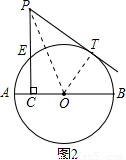：连接OP、OT．
在Rt△POT中，PT²=y，OT=1.5，则根据勾股定理知，PO²=PT²+OT²=y+2.25．
在Rt△PCO中，PC=2.5，OC=OA-x=1.5-x，则根据勾股定理知，PO²=PC²+OC²=6.25+（OT-x）²．
∴y+1.5²=6.25+（1.5-x）²，即y=x²-3x+6.25（0≤x≤1.5）；

（3））△PTC不可能变为以PC为斜边的等腰直角三角形．理由如下：
当△PTC变为以PC为斜边的等腰直角三角形时，PT⊥CT，
∵PT切⊙O于T，
∴CT过圆心，
∴CT就是⊙O的半径，即点C与圆心O重合（如图1所示）．
由（1）知，CT=1.5，PT=2，即PT≠CT，故△PTC不可能变为以PC为斜边的等腰直角三角形．
点评：本题考查了圆的综合题．其中涉及到的知识点有切线的性质、二次函数的解析式、等腰三角形的判定与性质以及勾股定理的应用．