Question

【题目】如图，在平面直角坐标系xOy中，抛物线y=x2+bx+c与y轴交于点C，与x轴交于A，B两点，点B的坐标为（3，0），直线y=﹣x+3恰好经过B，C两点

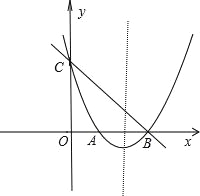
（1）写出点C的坐标；

（2）求出抛物线y=x2+bx+c的解析式，并写出抛物线的对称轴和点A的坐标；

（3）点P在抛物线的对称轴上，抛物线顶点为D且∠APD=∠ACB，求点P的坐标．

Answer 1

【答案】（1）C（0，3）；（2）y=x2﹣4x+3=（x-1）（x-3），对称轴为x=2，点A（1，0）；（3）（2，2）或（2，﹣2）

【解析】

试题分析：（1）由直线y=﹣x+3可求出C点坐标；

（2）由B，C两点坐标便可求出抛物线方程，从而求出抛物线的对称轴和A点坐标；

（3）作出辅助线OE，由三角形的两个角相等，证明△AEC∽△AFP，根据两边成比例，便可求出PF的长度，从而求出P点坐标．

试题解析：（1）y=﹣x+3与y轴交于点C，故C（0，3）．

（2）∵抛物线y=x2+bx+c过点B，C，

∴，

解得，

∴抛物线的解析式为y=x2﹣4x+3=（x﹣1）×（x﹣3），

∴对称轴为x=2，点A（1，0）．

（3）由y=x2﹣4x+3，

可得D（2，﹣1），A（1，0），

∴OB=3，OC=3，OA=1，AB=2，

可得△OBC是等腰直角三角形，

∴∠OBC=45°，．

如图，设抛物线对称轴与x轴交于点F，

∴AF=AB=1．

过点A作AE⊥BC于点E．

∴∠AEB=90度．

可得，．

在△AEC与△AFP中，∠AEC=∠AFP=90°，∠ACE=∠APF，

∴△AEC∽△AFP．

∴，

解得PF=2．

或者直接证明△ABC∽△ADP得出PD=3，

再得PF=2．

∵点P在抛物线的对称轴上，

∴点P的坐标为（2，2）或（2，﹣2）．