题目内容
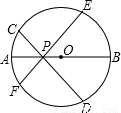
已知:如图,P为直径AB上一点,EF、CD为过点P的两条弦,且∠DPB=∠EPB.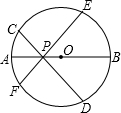
求证:
(1)CD=EF;
(2)
 |
| CE |
 |
| DF |
分析:(1)过点O作OM⊥EF于M,作ON⊥CD于N,根据全等三角形的判定方法得到△ODN≌△OEM,根据对应边相等,从而不难求得结论;
(2)根据CD=EF从而得到
=
由等量减去等量还是等量即可得到结论.
(2)根据CD=EF从而得到
 |
| CD |
 |
| EF |
解答:证明:(1)过点O作OM⊥EF于M,作ON⊥CD于N,连接OD、OE,
∵∠DPB=∠EPB,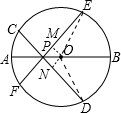
∴OM=ON.
又∵OE=OD,
∵∠OMP=∠ONP=90°,
∴Rt△ODN≌Rt△OEM(HL).
∴DN=EM.
∵OM⊥EF,ON⊥CD,
∴点M是EF的中点,点N是CD的中点.
∴EM=
EF,DN=
CD.
∴CD=EF.
(2)∵CD=EF,
∴
=
,
∴
-
=
-
.
即
=
.
∵∠DPB=∠EPB,

∴OM=ON.
又∵OE=OD,
∵∠OMP=∠ONP=90°,
∴Rt△ODN≌Rt△OEM(HL).
∴DN=EM.
∵OM⊥EF,ON⊥CD,
∴点M是EF的中点,点N是CD的中点.
∴EM=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=EF.
(2)∵CD=EF,
∴
 |
| CD |
 |
| EF |
∴
 |
| CD |
 |
| FC |
 |
| EF |
 |
| FC |
即
 |
| CE |
 |
| DF |
点评:本题利用了垂径定理和全等三角形的判定和性质及在同圆划等圆中,等弧对等弦,等弦对等弧求解.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
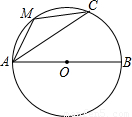
 已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为
已知:如图,AB为⊙O直径,AC为弦,M为弧AC上一点,若∠CAB=40度,则∠AMC的度数为
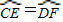 .
.