题目内容
如果直角三角形的一锐角是30°，斜边长是4cm，那么这个直角三角形的两条直角边长的和是（ ）
A、2（1+
| ||
B、(6+2
| ||
C、2（1+
| ||
| D、6cm |
分析：根据含30度角的直角三角形求出AC，根据勾股定理求出BC，相加即可．
解答：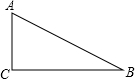
解：∵∠C=90°，∠B=30°，AB=4cm，
∴AC=
AB=2cm，
由勾股定理得：BC=
=2
cm，
∴AC+BC=2cm+2
cm=2（1+
）cm．
故选A．
解：∵∠C=90°，∠B=30°，AB=4cm，∴AC=
| 1 |
| 2 |
由勾股定理得：BC=
| AB2-AC2 |
| 3 |
∴AC+BC=2cm+2
| 3 |
| 3 |
故选A．
点评：本题主要考查对含30度角的直角三角形，勾股定理等知识点的理解和掌握，能根据性质求出AC、BC的长是解此题的关键．
练习册系列答案
相关题目
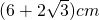
cm
cm
）cm
）cm
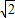）cm
）cm