��Ŀ����
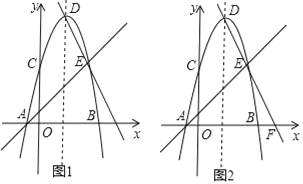
����Ŀ����ͼ1��ʾ����֪������y=��x2+bx+c��x�ύ��A����1��0����B��5��0�����㣬��y�ύ��C�㣬DΪ�����ߵĶ��㣬EΪ��������һ�㣬��C��E���������ߵĶԳ���Գƣ��ֱ���ֱ��AE��DE��
��1����˶��κ����Ĺ�ϵʽ��
��2����ͼ1�У�ֱ��DE����һ��Q��ʹ�á�QCO�ա�QBO�����Q�����ꣻ
��3����ͼ2��ֱ��DE��x�ύ�ڵ�F����MΪ�߶�AF��һ�����㣬��A��F�˶����ٶ�Ϊÿ��2����λ���ȣ��˶���F��ֹͣ����N��F��������������FE�����˶����ٶ�Ϊÿ��![]() ����λ���ȣ�M��N����ͬʱ�������˶�ʱ��Ϊt�룬��Mֹͣʱ��Nͬʱֹͣ�˶�����ƽ������һ������P��tΪ��ֵʱ����P��M��N��FΪ������ı����������ƽ���ı��Σ���ֱ��д��tֵ��
����λ���ȣ�M��N����ͬʱ�������˶�ʱ��Ϊt�룬��Mֹͣʱ��Nͬʱֹͣ�˶�����ƽ������һ������P��tΪ��ֵʱ����P��M��N��FΪ������ı����������ƽ���ı��Σ���ֱ��д��tֵ��
���𰸡���1�������ߵĽ���ʽΪ y=��x2+4x+5����2��Q�������Ϊ��![]() ��
�� ![]() ������3��t��ֵΪ
������3��t��ֵΪ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�������������������1��ֱ�����ý���ʽд�������ߵĽ���ʽ��
��2����ͼ1�������䷽���õ�D��2��9���������ߵĶԳ���Ϊֱ��x=2����ȷ��C��0��5������E��4��5�����������ô���ϵ�������ֱ��DE�Ľ���ʽΪy=��2x+13��Ȼ�����ȫ�������ε����ʵõ���COQ=��BOQ�����Ե�QΪ��һ����ƽ�����ϵĵ㣬���ⷽ����![]() ��Q������ꣻ
��Q������ꣻ
��3����ͼ2���Գ��ύx���ڵ�H����ȷ��DH=9��FH=![]() ��DF=
��DF=![]() ��AF=
��AF=![]() ��AM=2t��FN=
��AM=2t��FN=![]() t����FM=
t����FM=![]() ��2t���������ۣ�����P��M��N��FΪ������ı��������Σ���FM��FNΪ���ε����ڱߣ���FN=FM����
��2t���������ۣ�����P��M��N��FΪ������ı��������Σ���FM��FNΪ���ε����ڱߣ���FN=FM����![]() t=
t=![]() ��2t������P��M��N��FΪ������ı��������Σ���FNΪ���ζԽ��ߣ�����MP��FN��Q���������ε����ʵ�FQ=
��2t������P��M��N��FΪ������ı��������Σ���FNΪ���ζԽ��ߣ�����MP��FN��Q���������ε����ʵ�FQ=![]() t����ͨ���á�FQH�ס�FHD�õ�
t����ͨ���á�FQH�ס�FHD�õ�![]() t��
t�� ![]() =��
=��![]() ��2t����
��2t���� ![]() ������P��M��N��FΪ������ı��������Σ���FMΪ���ζԽ��ߣ�NP��MF�ཻ��K����ͼ3���������ε����ʵ�FK=
������P��M��N��FΪ������ı��������Σ���FMΪ���ζԽ��ߣ�NP��MF�ཻ��K����ͼ3���������ε����ʵ�FK=![]() ��
��![]() ��2t������ͨ����FKN�ס�FHD�õ�
��2t������ͨ����FKN�ס�FHD�õ�![]() ��
��![]() ��2t����
��2t���� ![]() =
=![]() t��
t�� ![]() ������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�NMF=90�㣬ͨ����FMN�ס�FHD�õ���
������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�NMF=90�㣬ͨ����FMN�ס�FHD�õ���![]() ��2t����
��2t���� ![]() =
=![]() t��
t�� ![]() ������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�MNF=90�㣬ͨ����FNM�ס�FHD�õ���
������P��M��N��FΪ������ı����Ǿ��Σ��ҡ�MNF=90�㣬ͨ����FNM�ס�FHD�õ���![]() ��2t����
��2t���� ![]() =
=![]() t��
t�� ![]() ��Ȼ��ֱ�����t�ķ��̿�ȷ������������t��ֵ��
��Ȼ��ֱ�����t�ķ��̿�ȷ������������t��ֵ��
�����������1�������ߵĽ���ʽΪy=����x+1����x��5������y=��x2+4x+5��
��2����ͼ1��y=��x2+4x+5=����x��2��2+9����D��2��9���������ߵĶԳ���Ϊֱ��x=2��
��x=0ʱ��y=��x2+4x+5=5����C��0��5����
��C��E���������ߵĶԳ���Գƣ�
��E��4��5����
��ֱ��DE�Ľ���ʽΪy=mx+n��
��D��2��9����E��4��5�������![]() �����
�����![]() ��
��
��ֱ��DE�Ľ���ʽΪy=��2x+13��
�ߡ�QCO�ա�QBO��
���COQ=��BOQ��
���QΪ��һ����ƽ�����ϵĵ㣬
��OQ�Ľ���ʽΪy=x��
�ⷽ����![]() �����
����� ��
��
��Q���������![]() ��
�� ![]() ����
����
��3����ͼ2���Գ��ύx���ڵ�H��DH=9��FH=![]() ��DF=
��DF=![]() ��
��
��y=0ʱ����2x+13=0�����x=![]() ����F��
����F��![]() ��0����
��0����
��AF=![]() ������1��=
������1��=![]() ��
��
AM=2t��FN=![]() t����FM=
t����FM=![]() ��2t��
��2t��
����P��M��N��FΪ������ı��������Σ���FM��FNΪ���ε����ڱߣ���FN=FM����![]() t=
t=![]() ��2t�����t=
��2t�����t=![]() ��
��
����P��M��N��FΪ������ı��������Σ���FNΪ���ζԽ��ߣ�����MP��FN��Q����PM��NQ���ഹֱƽ�֣�FQ=![]() t��
t��
�á�FQH�ס�FHD��
��FQ��FH=FM��FD����![]() t��
t�� ![]() =��
=��![]() ��2t����
��2t���� ![]() �����t=
�����t=![]() ��
��
����P��M��N��FΪ������ı��������Σ���FMΪ���ζԽ��ߣ�NP��MF�ཻ��K����ͼ3����MF��NP���ഹֱƽ�֣�FK=![]() MF=
MF=![]() ��
��![]() ��2t����
��2t����
�á�FKN�ס�FHD��
��FK��FH=FN��FD����![]() ��
��![]() ��2t����
��2t���� ![]() =
=![]() t��
t�� ![]() �����t=
�����t=![]() ��
��
����P��M��N��FΪ������ı����Ǿ��Σ��ҡ�NMF=90�㣬
�á�FMN�ס�FHD��
��FM��FH=FN��FD������![]() ��2t����
��2t���� ![]() =
=![]() t��
t�� ![]() �����t=
�����t=![]() ��
��
����P��M��N��FΪ������ı����Ǿ��Σ��ҡ�MNF=90�㣬
�á�FNM�ס�FHD��
��FM��FD=FN��FH������![]() ��2t����
��2t���� ![]() =
=![]() t��
t�� ![]() �����t=
�����t=![]() ��
��
����������t��ֵΪ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��