题目内容
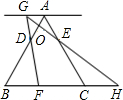 如图,已知:等边三角形ABC的边长为6,点D、E分别在边AB、AC上,且AD=AE=2.点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
如图,已知:等边三角形ABC的边长为6,点D、E分别在边AB、AC上,且AD=AE=2.点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.(1)用t的代数式表示AG;
(2)设△AGE的面积为S,写出S与t的函数关系式;
(3)当t为何值时,点F和点C是线段BH的三等分点?
分析:(1)根据平行线AG∥BC截线段成比例证得△ADG∽△BDF,然后由相似三角形的对应边成比例知
=
,从而求得AG=
t;
(2)作辅助线EK⊥AG构造直角三角形AEK,然后在直角三角形中求EK的长度;
(3)需分类讨论:①当点F在线段BC上时,若点F、点C是线段BH的三等分点;②当点F在BC的延长线上时,若点F、点C是线段BH的三等分点.
| AG |
| BF |
| AD |
| DB |
| 1 |
| 2 |
(2)作辅助线EK⊥AG构造直角三角形AEK,然后在直角三角形中求EK的长度;
(3)需分类讨论:①当点F在线段BC上时,若点F、点C是线段BH的三等分点;②当点F在BC的延长线上时,若点F、点C是线段BH的三等分点.
解答: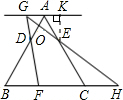 解:(1)∵AG∥BC,
解:(1)∵AG∥BC,
∴△ADG∽△BDF,
∴
=
,
又∵AD=2,DB=4,BF=t,
∴AG=
t;
(2)作EK⊥AG,垂足为K,
∵∠CAK=∠ACB=60°,
∴EK=AEsin60°=
,
S=
AG•EK=
t;
(3)①当点F在线段BC上时,若点F、点C是线段BH的三等分点,
则BF=FC=CH,BC=6,BF=3,
即当t=3时,点F、点C是BH的三等分点;
②当点F在BC的延长线上时,若点F、点C是线段BH的三等分点,
则BC=CF=FH,CF=6,BF=12,
即当t=12时,点F、点C是BH的三等分点.
 解:(1)∵AG∥BC,
解:(1)∵AG∥BC,∴△ADG∽△BDF,
∴
| AG |
| BF |
| AD |
| DB |
又∵AD=2,DB=4,BF=t,
∴AG=
| 1 |
| 2 |
(2)作EK⊥AG,垂足为K,
∵∠CAK=∠ACB=60°,
∴EK=AEsin60°=
| 3 |
S=
| 1 |
| 2 |
| ||
| 4 |
(3)①当点F在线段BC上时,若点F、点C是线段BH的三等分点,
则BF=FC=CH,BC=6,BF=3,
即当t=3时,点F、点C是BH的三等分点;
②当点F在BC的延长线上时,若点F、点C是线段BH的三等分点,
则BC=CF=FH,CF=6,BF=12,
即当t=12时,点F、点C是BH的三等分点.
点评:本题综合考查了解直角三角形、等边三角形的性质、相似三角形的性质与判定.在解答第(3)题时,要分类讨论,以防漏解.

练习册系列答案
相关题目