题目内容
(1)计算:2-1-tan60°+( -1)0
-1)0
(2)解方程: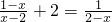 .
.
解:(1)原式= -
- +1=
+1= -
- ;
;
(2)方程的两边同乘(x-2),得
1-x+2(x-2)=-1,
解得x=2.
检验:把x=2代入(x-2)=0,所以x=2是原方程的增根,
故原方程无解.
分析:(1)本题主要考查的对象有零指数幂、负指数幂、特殊角的三角函数值3个考点.在计算时分别对其求解,然后运用实数的运算法计算结果;
(2)观察可得最简公分母是(x-2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
点评:本题考查了实数的综合运算能力及分式方程的解法.进行实数的运算时,关键是掌握零指数幂、负指数幂、特殊角的三角函数值等考点的运算;解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解,同时解分式方程一定注意要验根.
 -
- +1=
+1= -
- ;
;(2)方程的两边同乘(x-2),得
1-x+2(x-2)=-1,
解得x=2.
检验:把x=2代入(x-2)=0,所以x=2是原方程的增根,
故原方程无解.
分析:(1)本题主要考查的对象有零指数幂、负指数幂、特殊角的三角函数值3个考点.在计算时分别对其求解,然后运用实数的运算法计算结果;
(2)观察可得最简公分母是(x-2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
点评:本题考查了实数的综合运算能力及分式方程的解法.进行实数的运算时,关键是掌握零指数幂、负指数幂、特殊角的三角函数值等考点的运算;解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解,同时解分式方程一定注意要验根.

练习册系列答案
相关题目