题目内容
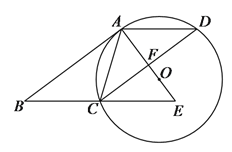
【题目】如图,在□ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交于E.
(1)求证:AB是⊙O的切线;
(2)若AB=8,AD=5,求OE的长.
【答案】(1)证明参见解析;(2)![]() .
.
【解析】试题分析:(1)由已知得出弧AC=弧AD,由垂径定理得出OA⊥CD,由平行四边形的性质得出AB∥CD,AD∥BC,AD=BC,因此OA⊥AB,即可得出结论;(2)连接OD,由垂径定理得出CF=DF=4,由平行线得出△ADF∽△ECF,得出对应边成比例,证出AD=CE,AF=EF,得出BC=CE,BE=10,由勾股定理求出AE,得出AF=EF=3,设OE=x,则OF=3﹣x,⊙O的半径为6﹣x,由勾股定理得出方程,解方程即可.
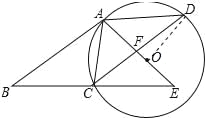
试题解析:(1)∵AC=AD,∴弧AC=弧AD,∴OA⊥CD,∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,AD=BC,∴OA⊥AB,∴AB是⊙O的切线;(2)连接OD,如图所示:∵OA⊥CD,∴CF=DF=4,∵AD∥BC,∴△ADF∽△ECF,∴![]() =1,∴AD=CE,AF=EF,∴BC=CE,∴BE=2BC=2AD=10,∴AE=
=1,∴AD=CE,AF=EF,∴BC=CE,∴BE=2BC=2AD=10,∴AE=![]() =6,∴AF=EF=3,设OE=x,则OF=3﹣x,⊙O的半径为6﹣x,由勾股定理得:OF2+DF2=OD2,即(6﹣x)2=(3﹣x)2+42,解得:x=
=6,∴AF=EF=3,设OE=x,则OF=3﹣x,⊙O的半径为6﹣x,由勾股定理得:OF2+DF2=OD2,即(6﹣x)2=(3﹣x)2+42,解得:x=![]() ,即OE=
,即OE=![]() .
.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目