题目内容
【题目】如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线BD上有一点P,使PC+PE的和最小,则这个最小值为( )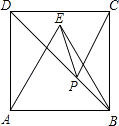
A.4
B.2 ![]()
C.2 ![]()
D.2
【答案】A
【解析】解:∵正方形ABCD,
∴AC⊥BD,OA=OC,
∴C.A关于BD对称,
即C关于BD的对称点是A,
连接AE交BD于P,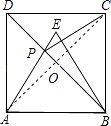
则此时EP+CP的值最小,
∵C.A关于BD对称,
∴CP=AP,
∴EP+CP=AE,
∵等边三角形ABE,
∴EP+CP=AE=AB,
∵正方形ABCD的面积为16,
∴AB=4,
∴EP+CP=4,
故答案为:A.
根据正方形的性质和轴对称的性质可知:EP+CP的最小值=AE=AB,而正方形ABCD的面积为16,则AB=4。

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目