题目内容
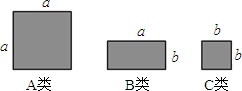
如图，有足够多的边长为a的大正方形、长为a宽为b的长方形以及边长为b的小正方形．（1）取其中的若干个（三种图形都要取到）拼成一个长方形，使其面积为（a+b）（a+2b），画出图形，并根据图形回答（a+b）（a+2b）=______．
（2）取其中的若干个（三种图形都要取到）拼成一个长方形，使其面积为a2+5ab+4b2，
①需要A类卡片______张、B类卡片______张、C类卡片______张．
②可将多项式a2+5ab+4b2分解因式为______．
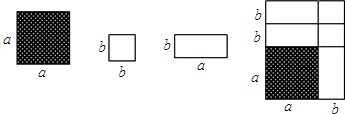解：（1）如图可知：（a+b）（a+2b）=a2+3ab+2b2；（2）一个长方形，使其面积为a2+5ab+4b2，
①需要A类卡片1张、B类卡片5张、C类卡片4张．
②a2+5ab+4b2=（a+b）（a+4b）．
故答案为：1、5、4；（a+b）（a+4b）．
分析：（1）由图中大矩形的面积=中间的各图片的面积的和，就可得出代数式．
（2）拼法较多，可根据小图片的面积和要拼成的大矩形的面积进行比较可得出需要的小图片的张数．再根据长方形的面积分解因式．
点评：本题主要考查了分解因式与几何图形之间的联系，从几何的图形来解释分解因式的意义．解此类题目的关键是正确的分析图形，找到组成图形的各个部分，并用面积的两种求法作为相等关系列式子．
练习册系列答案
相关题目
21、如图，有足够多的边长为a的大正方形、长为a宽为b的长方形以及边长为b的小正方形．（1）取其中的若干个（三种图形都要取到）拼成一个长方形，使其面积为（a+b）（a+2b），画出图形，并根据图形回答（a+b）（a+2b）=
如图，有足够多的边长为a的小正方形（A类）、长为a宽为b的长方形（B类）以及边长为b的大正方形（C类），发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式．
