题目内容
一次函数y=k x+b的图像经过点(0,-4)且与正比例函数y=k
x+b的图像经过点(0,-4)且与正比例函数y=k x的图象交于点(2,-1).
x的图象交于点(2,-1).
(1)分别求出这两个函数的表达式;
(2)求这两个函数的图象与x轴围成的三角形的面积;
(3)直接写出不等式k x-4≥k
x-4≥k x的解集。
x的解集。
 x+b的图像经过点(0,-4)且与正比例函数y=k
x+b的图像经过点(0,-4)且与正比例函数y=k x的图象交于点(2,-1).
x的图象交于点(2,-1).(1)分别求出这两个函数的表达式;
(2)求这两个函数的图象与x轴围成的三角形的面积;
(3)直接写出不等式k
 x-4≥k
x-4≥k x的解集。
x的解集。(1) ,y=
,y= ;(2)
;(2) ;(3)x≥2
;(3)x≥2
 ,y=
,y= ;(2)
;(2) ;(3)x≥2
;(3)x≥2试题分析:(1)由一次函数y=k
 x+b的图像经过点(0,-4)且与正比例函数y=k
x+b的图像经过点(0,-4)且与正比例函数y=k x的图象交于点(2,-1)根据待定系数法即可求得结果;
x的图象交于点(2,-1)根据待定系数法即可求得结果;(2)先求出一次函数
 与x轴的交点坐标,再根据三角形的面积公式求解即可;
与x轴的交点坐标,再根据三角形的面积公式求解即可;(3)根据两个函数图象的交点坐标再结合一次函数的性质即可作出判断.
(1)∵y=kx+b经过点(0,-4)和(2,-1)
∴b=-4,2k-4=-1
解得k=

∴

∵y=kx经过点(2,-1)
∴k=

∴y=
 ;
;(2)
 与x轴的交点为(
与x轴的交点为( ,0)
,0) ∴S=

(3)由题意得不等式k
 x-4≥k
x-4≥k x的解集为x≥2.
x的解集为x≥2.点评:此类问题是初中数学的重点,是中考常见题,一般难度不大,需熟练掌握.

练习册系列答案
相关题目
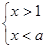 无解,则a的取值范围是 ( )
无解,则a的取值范围是 ( )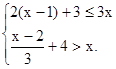 的整数解.
的整数解. ,若
,若 为整数时,方程组
为整数时,方程组 的解
的解 为正数,
为正数, 为负数,则a的值为( )
为负数,则a的值为( ) 的正整数解是_______________________.
的正整数解是_______________________. ,若
,若 为实数,则下列不等式中成立的是( ).
为实数,则下列不等式中成立的是( ).
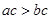


 的最小整数解是 .
的最小整数解是 . 的解集是
的解集是 ,求不等式
,求不等式 的解集。
的解集。 、
、 的方程组
的方程组 的解都是非正数,求
的解都是非正数,求 的取值范围.
的取值范围.