Question

等边三角形的周长为18，则它的内切圆半径是（　　）

• A、2

  3

• B、3

  3

• C、

  3

• D、

  3

  2

Answer 1

分析：首先根据题意作出图形，然后连接OB，OD，由等边△ABC是⊙O的内接圆，△ABC的周长为18，根据正三角形内切圆的性质，即可求得它的内切圆半径．

解答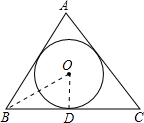：解：连接OB，OD，
∵等边△ABC是⊙O的内接圆，△ABC的周长为18，
∴∠ABC=60°，BC=6，
∴OD⊥BC，∠OBD=

1

2

∠ABC=

1

2

×60°=30°，BD=

1

2

BC=3，
∴OD=BD•tan∠OBD=3×

3

3

=

3

．
∴它的内切圆半径是：

3

．
故选C．

点评：此题考查了正三角形的性质与三角形内接圆的性质．此题难度不大，解题的关键是注意数形结合思想的应用，注意辅助线的作法．