题目内容
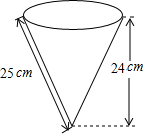
g图，Rt△地BC中地C=图，BC=3，绕其中一条线段旋转一周，所得图形的最小表面积是______．
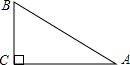
当以A四为轴，则由AC=4，四C=3，由勾股定理得，A四=5，斜边z的高=
，
由几何体是由两个圆锥组成，∴几何体的表面积=
×2×
π×（3+4）=
π，
当以四C为轴，几何体的表面积=π×4×5+π×42=38π，
当以AC为轴，几何体的表面积=π×3×5+π×32=24π，
∴绕其中A四旋转一周，所得图形的最小表面积是：
π．
故答案为：
π．
| 12 |
| 5 |
由几何体是由两个圆锥组成，∴几何体的表面积=
| 1 |
| 2 |
| 12 |
| 5 |
| 84 |
| 5 |
当以四C为轴，几何体的表面积=π×4×5+π×42=38π，
当以AC为轴，几何体的表面积=π×3×5+π×32=24π，
∴绕其中A四旋转一周，所得图形的最小表面积是：
| 84 |
| 5 |
故答案为：
| 84 |
| 5 |
练习册系列答案
名校课堂系列答案
相关题目
