题目内容
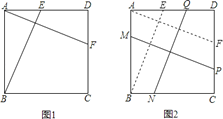
【题目】(10分)如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
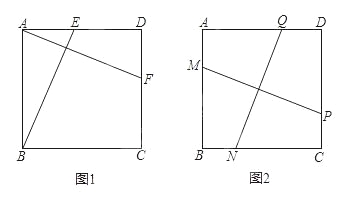
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
【答案】(1)证明:如图(1),在正方形ABCD中,AB=DA,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°,
∵AF⊥BE,∴∠ABE+∠BAF=90°,∴∠ABE=∠DAF,
∵在△ABE和△DAF中, 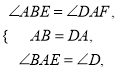
∴△ABE≌△DAF(ASA),∴BE=AF.
(2)解:MP与NQ相等.理由如下:
如图(2),过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,则BE=NQ,AF=MP.只需证BE=AF即可.与(1)的情况完全相同.

【解析】试题分析:(1)要证明AF=BE成立,只需要根据条件证明△ABE≌△DAF即可;(2)过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,将问题转化为证明AF=BE,即可应用(1)的结论.
试题解析:(1)证明:在正方形ABCD中,AB=AD,∠BAE=∠D=90°,
∴∠DAF+∠BAF=90°,∵AF⊥BE,∴∠ABE+∠BAF=90°,
∴∠ABE=∠DAF,∵在△ABE和△DAF中,
 ,∴△ABE≌△DAF(ASA),∴AF=BE;
,∴△ABE≌△DAF(ASA),∴AF=BE;
(2)解:MP与NQ相等.
理由如下:如图,过点A作AF∥MP交CD于F,过点B作BE∥NQ交AD于E,
由(1)可知MP=NQ.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目