题目内容
【题目】如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:

(1)求线段AB的长及⊙C的半径;
(2)求B点坐标及圆心C的坐标。
【答案】(1)4,2;(2)B(![]() ,0),C(
,0),C(![]() ,1).
,1).
【解析】
试题(1)连接AB,判断出∠OAB=60°,从而得到∠OBA=30°,根据AB=2OA=4,可求出 C的半径r=2.
(2)在Rt△OAB中,由勾股定理得到OB的长,再根据垂径定理求出OE、OF的长,从而得到C点坐标.
试题解析:(1)∵∠ODB=∠OAB,∠ODB=60°
∴∠OAB=60°,
∵∠AOB是直角,
∴AB是⊙C的直径,∠OBA=30°
∴AB=2OA=4,
∴⊙C的半径r=2
(2)在Rt△OAB中,由勾股定理得:OB2+ OA2= AB2,
∴OB=![]() ,
,
∴B的坐标为:(![]() ,0)
,0)
过C点作CE⊥OA于E,CF⊥OB于F,

由垂径定理得: OE=AE=1,OF=BF=![]() ,
,
∴CE=![]() ,CF=1,
,CF=1,
∴C的坐标为(![]() ,1)
,1)

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】王老师将1个黑球和若干个白球入放一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球(有放回),统计数据如下表:
摸球的次数(n) | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数(m) | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率(m/n) | 0.230 | 0.207 | 0.300 | 0.260 | 0.254 |
(1)补全上表中的有关数据,并根据上表数据估计从袋中摸出一个球是黑球的概率是 ;
(2)估计口袋中白球的个数;
(3)在(2)的条件下,若小强同学有放回地连续两次摸球,用画树状图法或列表法计算他两次都摸出白球的概率。
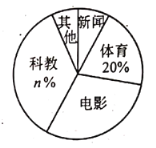
【题目】学校为了解全校![]() 名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
名学生双休日在家最爱选择的电视频道情况,问卷要求每名学生从“新闻,体育,电影,科教,其他”五项中选择其一,随机抽取了部分学生,调查结果绘制成未完成的统计图表如下:
频道 | 新闻 | 体育 | 电影 | 科教 | 其他 |
人数 |
|
|
|
|
|
![]() 求调查的学生人数及统计图表中
求调查的学生人数及统计图表中![]() 的值;
的值;
![]() 求选择其他频道在统计图中对应扇形的圆心角的度数;
求选择其他频道在统计图中对应扇形的圆心角的度数;
![]() 求全校最爱选择电影频道的学生人数.
求全校最爱选择电影频道的学生人数.