题目内容
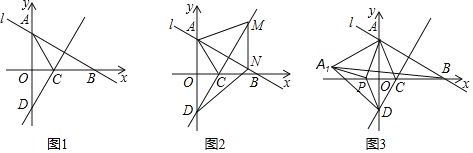
【题目】如图1,在平面直角坐标系中,已知直线l:y![]() x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.
x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.
(1)求直线CD的解析式;
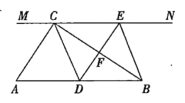
(2)如图2,若点M为直线CD上的一个动点,过点M作MN∥y轴,交直线AB与点N,当四边形AMND为菱形时,求△ACM的面积;
(3)如图3,点P为x轴上的一个动点连接PA、PD,将△ADP沿DP翻折得到△A1DP,当以点A、A1、B为顶点的三角形是等腰三角形时,求点P的坐标.
【答案】(1)y![]() x﹣3;(2)
x﹣3;(2)![]() ;(3)点P的坐标为(
;(3)点P的坐标为(![]() ,0),(﹣6﹣3
,0),(﹣6﹣3![]() ),(3
),(3![]() ,0),(6﹣3
,0),(6﹣3![]() ,0).
,0).
【解析】
(1)分别令x、y为0,建立方程可求得A、B的坐标,并由tan∠BAO=![]() ,求得∠BAO=60°,由AC平分∠BAO求得C的坐标,再应用两条直线垂直时,k1k2=-1,就可以求得CD的解析式;
,求得∠BAO=60°,由AC平分∠BAO求得C的坐标,再应用两条直线垂直时,k1k2=-1,就可以求得CD的解析式;
(2)根据菱形对角线互相垂直平分这一性质,可以确定点M的坐标,易求出△ACM的面积;
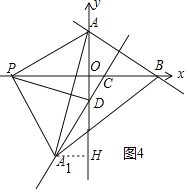
(3)△AA1B为等腰三角形,分三种情况:①AA1=AB,证明△ADA1是等边三角形解决问题.②A1B=AB.过A1作A1H⊥y轴于H,易证△A1AH≌△APO(AAS),利用全等三角形性质解决问题即可.③AA1=A1B.若点P在x负半轴上,不存在A1B=AB,若点P在x正半轴上,点P与点B重合时,A1B=AB.
(1)如图1,
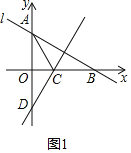
在y![]() x+3中,令x=0,得y=3,
x+3中,令x=0,得y=3,
∴A(0,3),
令y=0得0![]() x+3,解得x=3
x+3,解得x=3![]() ,
,
∴B(3![]() ,0),
,0),
在Rt△AOB中,∠AOB=90°,
∴∠BAO=60°,
∵AC平分∠BAO,
∴∠CAO![]() ∠BAO=30°
∠BAO=30°
∴OC![]()
∴C(![]() ,0)
,0)
∵CD⊥AB
∴∠ODC=90°﹣∠BAO=90°﹣60°=30°
在Rt△COD中,∠COD=90°,
∴OD=3
∴D(0,﹣3)
设直线CD解析式为y=kx+b,将C(![]() ,0),D(0,﹣3)代入得
,0),D(0,﹣3)代入得
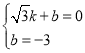 ,解得
,解得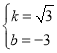
∴直线CD的解析式为y![]() x﹣3.
x﹣3.
(2)如图2,
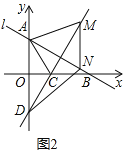
令CD与AB交于点E,∵四边形AMND是菱形,
∴AE=NE DE=ME
解方程组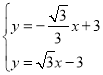 得
得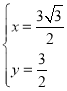 ,
,
∴E(![]() ,
,![]() ),
),
设M(t,![]() t﹣3),则
t﹣3),则![]() ,
,![]() ,∴t=3
,∴t=3![]()
∴M(![]() ,6),
,6),
在Rt△ADE中,cos∠ODC![]() ,sin∠ODC
,sin∠ODC![]()
∴DE=AD×cos∠ODC=6cos30°=3![]() ,AE=ADsin∠ODC=6sin30°=3
,AE=ADsin∠ODC=6sin30°=3
∴![]()
在Rt△ODC中,∠ODC=30°,∴CD=2OC=2![]()
∴CE=DE﹣CD=3![]() 2
2![]()
∴CM=CE+ME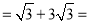 4
4![]() ,
,
∴S△ACM![]() .
.
(3)如图3,
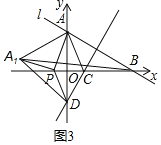
△AA1B为等腰三角形,分三种情况:
①AA1=AB,
由翻折知:A1D=AD=6,A1P=AP,∠ADP=∠A1DP,
∵∠ABO=90°﹣∠BAO=90°﹣60°=30°,
∴AB=2AO=2×3=6
∴AA1=A1D=AD
∴△AA1D是等边三角形
∴∠A1DA=60°,
∴∠ADP=30°,在Rt△PDO中,tan∠ADP![]()
∴OP=OD×tan∠ADP=3tan30°![]()
∴![]()
②AA1=A1B
∴A1在线段AB垂直平分线,
易证直线CD垂直平分线段AB
∴点A1落在直线CD上
由翻折知:A1D=AD=6,A1P=AP,∠ADP=∠A1DP,
∵∠ADC=30°,
∴∠ADP=∠A1DP=75°,∠DPO=90°﹣∠ADP=90°﹣75°=15°,
∵OA=OD,PO⊥AD
∴∠APO=∠DPO=15°,
∴∠APD=∠A1PD=30°
∴∠A1PA=60°
∴△A1PA是等边三角形
∴AP=A1A
过A1作A1H⊥y轴于H,易证△A1AH≌△APO(AAS)
A1H=AO=3,AH=OP
点A1B的横坐标为﹣3,将x=﹣3代入直线CD的解析式为y![]() x﹣3中,得y=﹣3
x﹣3中,得y=﹣3![]() 3,
3,
∴OH=3![]() 3,OP=AH=AO+OH=3+3
3,OP=AH=AO+OH=3+3![]() 3=6+3
3=6+3![]() ,
,
∴P(﹣6﹣3![]() ,0)
,0)
③A1B=AB
若点P在x负半轴上,不存在A1B=AB,
若点P在x正半轴上,点P与点B重合时,A1B=AB
∴P(3![]() ,0),
,0),
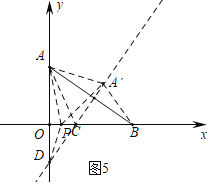
④如图5中,当AA′=A′B时,易证DP平分∠ODC,可得P(6﹣3![]() ,0)
,0)
综上所述,点P的坐标为(![]() ,0),(﹣6﹣3
,0),(﹣6﹣3![]() ),(3
),(3![]() ,0),(6﹣3
,0),(6﹣3![]() ,0).
,0).