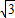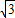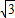题目内容
已知P为边长是2的正六边形ABCDEF内一点,P点到各边的距离分别为h1、h2、h3 h4、h5、h6,则h1+h2+h3+h4+h5+h6=
- A.2

- B.4

- C.6

- D.8

C
分析:根据题意画出图形,易得S正六边形ABCDEF= ×2(h1+h2+h3+h4+h5+h6),过正六边形的中心O作OG⊥BC于点G,则S正六边形ABCDEF=6×
×2(h1+h2+h3+h4+h5+h6),过正六边形的中心O作OG⊥BC于点G,则S正六边形ABCDEF=6× ×2OG=6OG,故h1+h2+h3+h4+h5+h6=6OG,再由等边三角形
×2OG=6OG,故h1+h2+h3+h4+h5+h6=6OG,再由等边三角形
解答: 解:如图所示,
解:如图所示,
∵P为边长是2的正六边形ABCDEF内一点,P点到各边的距离分别为h1、h2、h3 h4、h5、h6,
∴S正六边形ABCDEF= ×2(h1+h2+h3+h4+h5+h6),
×2(h1+h2+h3+h4+h5+h6),
过正六边形的中心O作OG⊥BC于点G,则S正六边形ABCDEF=6× ×2OG=6OG,
×2OG=6OG,
∴h1+h2+h3+h4+h5+h6=6OG,
∵∠OBC=60°,OG⊥BC,
∴BG= BC=2,OG=BG•tan60°=1×
BC=2,OG=BG•tan60°=1× =
= ,
,
∴h1+h2+h3+h4+h5+h6=6OG=6× =6
=6 .
.
故选C.
点评:本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.
分析:根据题意画出图形,易得S正六边形ABCDEF=
 ×2(h1+h2+h3+h4+h5+h6),过正六边形的中心O作OG⊥BC于点G,则S正六边形ABCDEF=6×
×2(h1+h2+h3+h4+h5+h6),过正六边形的中心O作OG⊥BC于点G,则S正六边形ABCDEF=6× ×2OG=6OG,故h1+h2+h3+h4+h5+h6=6OG,再由等边三角形
×2OG=6OG,故h1+h2+h3+h4+h5+h6=6OG,再由等边三角形解答:
 解:如图所示,
解:如图所示,∵P为边长是2的正六边形ABCDEF内一点,P点到各边的距离分别为h1、h2、h3 h4、h5、h6,
∴S正六边形ABCDEF=
 ×2(h1+h2+h3+h4+h5+h6),
×2(h1+h2+h3+h4+h5+h6),过正六边形的中心O作OG⊥BC于点G,则S正六边形ABCDEF=6×
 ×2OG=6OG,
×2OG=6OG,∴h1+h2+h3+h4+h5+h6=6OG,
∵∠OBC=60°,OG⊥BC,
∴BG=
 BC=2,OG=BG•tan60°=1×
BC=2,OG=BG•tan60°=1× =
= ,
,∴h1+h2+h3+h4+h5+h6=6OG=6×
 =6
=6 .
.故选C.
点评:本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目