题目内容
在直角坐标系中有三点A(0,-1),B(1,3)C(2,6).已知直线y=ax+b上横坐标为0,1,2的点分别为D,E,F,试求a,b的值使AD2+BE2+CF2达到最小值 .
【答案】分析:先求出D(0,b),E(1,a+b),F(2,2a+b),根据坐标可列出AD、BE、CF的表达式.
解答:解:由题意可得:D(0,b),E(1,a+b),F(2,2a+b),
∴AD2+BE2+CF2=(b+1)2+(a+b-3)2+(2a+b-6)2,
=(b+1)2+[(a-3)+b]2+[2(a-3)+b]2,
=3b2+2b+1+5(a-3)2+6(a-3)b,
=5[a-3+(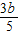 )]2+
)]2+ b2+2b+1,
b2+2b+1,
=5[a-3+(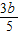 )]2+
)]2+ (b+
(b+ )2+
)2+ ,
,
∴a-3+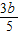 =0,b+
=0,b+ =0.
=0.
解得a= ,b=-
,b=- 时,有最小值为
时,有最小值为 .
.
故答案为: .
.
点评:此题考查了函数图象上点的坐标特征,将AD2+BE2+CF2转化为完全平方式,再根据非负数的性质求出最值是常用的方法.
解答:解:由题意可得:D(0,b),E(1,a+b),F(2,2a+b),
∴AD2+BE2+CF2=(b+1)2+(a+b-3)2+(2a+b-6)2,
=(b+1)2+[(a-3)+b]2+[2(a-3)+b]2,
=3b2+2b+1+5(a-3)2+6(a-3)b,
=5[a-3+(
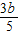 )]2+
)]2+ b2+2b+1,
b2+2b+1,=5[a-3+(
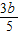 )]2+
)]2+ (b+
(b+ )2+
)2+ ,
,∴a-3+
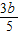 =0,b+
=0,b+ =0.
=0.解得a=
 ,b=-
,b=- 时,有最小值为
时,有最小值为 .
.故答案为:
 .
.点评:此题考查了函数图象上点的坐标特征,将AD2+BE2+CF2转化为完全平方式,再根据非负数的性质求出最值是常用的方法.

练习册系列答案
相关题目