题目内容
【题目】如图1，正方形纸片ABCD的边长为2，翻折∠B、∠D，使两个直角的顶点重合于对角线BD上一点P，EF、GH分别是折痕（如图2）．设AE=x（0＜x＜2），给出下列判断：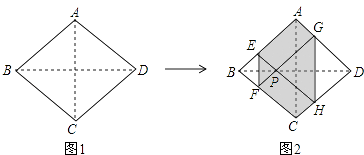 
①当x=1时，点P是正方形ABCD的中心；
②当x= 
时，EF+GH＞AC；
③当0＜x＜2时，六边形AEFCHG面积的最大值是 
；
④当0＜x＜2时，六边形AEFCHG周长的值不变．
其中正确的是（写出所有正确判断的序号）．
【答案】①④
【解析】解：（1）正方形纸片ABCD，翻折∠B、∠D，使两个直角的顶点重合于对角线BD上一点P，
∴△BEF和△DGH是等腰直角三角形，
∴当AE=1时，重合点P是BD的中点，
∴点P是正方形ABCD的中心；
故①结论正确，（2）正方形纸片ABCD，翻折∠B、∠D，使两个直角的顶点重合于对角线BD上一点P，
∴△BEF∽△BAC，
∵x= 
，
∴BE=2﹣ = 
，
∴ 
= 
，即 
= ，
∴EF= 
AC，
同理，GH= 
AC，
∴EF+GH=AC，
故②结论错误，（3）六边形AEFCHG面积=正方形ABCD的面积﹣△EBF的面积﹣△GDH的面积．
∵AE=x，
∴六边形AEFCHG面积=22﹣ BEBF﹣ GDHD=4﹣ ×（2﹣x）（2﹣x）﹣ xx=﹣x2+2x+2=﹣（x﹣1）2+3，
∴六边形AEFCHG面积的最大值是3，
故③结论错误，（4）当0＜x＜2时，
∵EF+GH=AC，
六边形AEFCHG周长=AE+EF+FC+CH+HG+AG=（AE+CH）+（FC+AG）+（EF+GH）=2+2+2 
=4+2
故六边形AEFCHG周长的值不变，
故④结论正确．
所以答案是：①④．
【考点精析】本题主要考查了正方形的性质和翻折变换（折叠问题）的相关知识点，需要掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能正确解答此题．
