题目内容
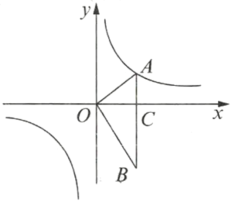
【题目】如图,在平面直角坐标系中,![]() ,
,![]() 轴于点
轴于点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上.
的图像上.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求![]() 面积;
面积;
(3)在坐标轴上是否存在一点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰三角形,若存在,请直接写出所有符合条件的点
三点为顶点的三角形是等腰三角形,若存在,请直接写出所有符合条件的点![]() 的坐标;若不存在,简述你的理由.
的坐标;若不存在,简述你的理由.
【答案】(1)![]() (2)
(2)![]() (3)存在,点P的坐标为(
(3)存在,点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(0,
,0)或(0,![]() )或(0,
)或(0,![]() )或(0,6)或(0,2).
)或(0,6)或(0,2).
【解析】
(1)根据点A的坐标,利用待定系数法可求出反比例函数的表达式;
(2)由点A的坐标可得出OC,AC的长,利用勾股定理可得出OA=2=2AC,进而可得出∠AOC=30°,结合三角形内角和定理可得出∠B=∠AOC=30°,利用30°角所对的直角边为斜边的一半可求出AB的长,再利用三角形的面积公式即可求出△AOB的面积;
(3)根据勾股定理可求出OB的长,分OP=OB,BP=BO及PO=PB三种情况,利用等腰三角形的性质可求出点P的坐标,此题得解.
(1)把![]() 代入反比例函数
代入反比例函数![]() ,得:
,得:![]() ,
,
所以反比例函数的表达式为![]() ;
;
(2)![]() ,
,![]() 轴于
轴于![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
∴∠OAC=60°,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)存在,
在Rt△AOB中,OA=2,AB=4,∠AOB=90°,
∴OB=![]() ,
,
分三种情况考虑:
①当OP=OB时,如图2所示,
∵OB=![]() ,
,
∴OP=![]() ,
,
∴点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(0,
,0)或(0,![]() )或(0,
)或(0,![]() );
);
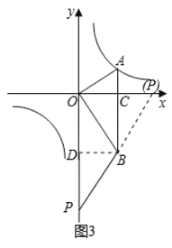
②当BP=BO时,如图3,
当点P在y轴上时,过点B做BD⊥y轴于点D,则OD=BC=ABAC=3,
∵BP=BO,
∴OP=2OD=6,
∴点P的坐标为(0,6);
当点P在x轴上时,
∵BP=BO,
∴OP=2OC=![]() ,
,
∴点P的坐标为(![]() ,0);
,0);
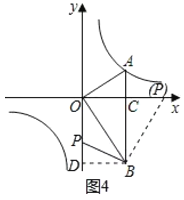
③当PO=PB时,如图4所示.
若点P在x轴上,∵PO=PB,∠BOP=60°,
∴△BOP为等边三角形,
∴OP=OB=![]() ,
,
∴点P的坐标为(![]() ,0);
,0);
若点P在y轴上,设OP=a,则PD=3a,
∵PO=PB,
∴PB2=PD2+BD2,即a2=(3a)2+3,
解得:a=2,
∴点P的坐标为(0,2),
综上所述:在坐标轴上存在一点P,使得以O、B、P三点为顶点的三角形是等腰三角形,点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(0,
,0)或(0,![]() )或(0,
)或(0,![]() )或(0,6)或(0,2).
)或(0,6)或(0,2).


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案【题目】现在要从甲、乙两名学生中选择一名学生去参加比赛,因甲乙两人的5次测试总成绩相同,所以根据他们的成绩绘制了尚不完整的统计图表进行分析.
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 90 | 70 | 80 | 100 | 60 |
乙成绩 | 70 | 90 | 90 | a | 70 |
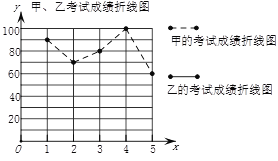
请同学们完成下列问题:
(1)a=________,![]() =________;
=________;
(2)请在图中完成表示乙成绩变化情况的折线:
(3)S2甲=200,请你计算乙的方差;
(4)可看出________将被选中参加比赛.(第1问和第4问答案可直接填写在答题卡的横线上)