��Ŀ����
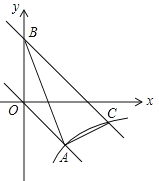
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��l��������![]() �ཻ��A��1��
�ཻ��A��1��![]() ����B��4��0�����㣮
����B��4��0�����㣮
��1����������ߵĽ���ʽ��
��2�������������Ƿ���ڵ�D��ʹ�á�ABD�����߶�ABΪб�ߵ�ֱ�������Σ������ڣ������D�����ꣻ�������ڣ�˵�����ɣ�
��3����P���߶�AB��һ���㣬����P�����A��B�غϣ�������P��PM��OA������һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������BCN����PMN�����S��BCN��S��PMN����S��BCN=2S��PMN�����![]() ��ֵ���������ʱ��M�����꣮
��ֵ���������ʱ��M�����꣮
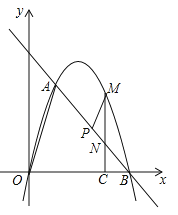
���𰸡���1��![]() ����2��D��1��0������0��
����2��D��1��0������0��![]() ����0��
����0��![]() ������3��
������3��![]() ��M��
��M��![]() ��
��![]() ����
����
��������
�����������1����A��B��������꣬���ô���ϵ��������������߽���ʽ��
��2����D��x���Ϻ�y���ϣ���D��x����ʱ����A��AD��x�ᣬ����D��Ϊ����D����y����ʱ�����D������Ϊ��0��d�����ɷֱ��ʾ��AD��BD�������ù��ɶ����ɵõ�����d�ķ��̣������d��ֵ���Ӷ����������������D�����ꣻ
��3����P��PF��CM�ڵ�F������Rt��ADO��Rt��MFP�Լ����Ǻ���������PF�ֱ��ʾ��MF��NF���Ӷ��ɱ�ʾ��MN����BC=a�������a��ʾ��CN��������S��BCN=2S��PMN������PF��ʾ��a��ֵ���Ӷ�����PF��ʾ��CN�������![]() ��ֵ������a�ɱ�ʾ��M������꣬���������߽���ʽ�����a��ֵ���Ӷ������M������꣮
��ֵ������a�ɱ�ʾ��M������꣬���������߽���ʽ�����a��ֵ���Ӷ������M������꣮
���������
��1����A��1��![]() ����B��4��0����������
����B��4��0����������![]() ��ͼ���ϣ���
��ͼ���ϣ��� �����
�����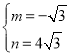 ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
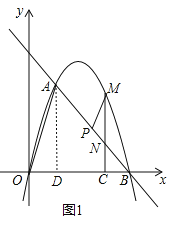
��2�������������������⣬�������£�
������D��x����ʱ����ͼ1������A��AD��x���ڵ�D����A��1��![]() ������D����Ϊ��1��0����
������D������1��0����
������D��y����ʱ����D��0��d������![]() ��
��![]() ����
����![]() ���ߡ�ABD����ABΪб�ߵ�ֱ�������Σ���
���ߡ�ABD����ABΪб�ߵ�ֱ�������Σ���
![]() ����
����![]() �����d=
�����d=![]() ����D��������0��
����D��������0��![]() ����0��
����0��![]() ����
����
���Ͽ�֪��������������D�㣬������Ϊ��1��0������0��![]() ����0��
����0��![]() ����
����
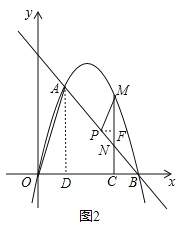
��3����ͼ2����P��PF��CM�ڵ�F����PM��OA����Rt��ADO��Rt��MFP����![]() =
=![]() ����MF=
����MF=![]() PF����Rt��ABD��BD=3��AD=
PF����Rt��ABD��BD=3��AD=![]() ����tan��ABD=
����tan��ABD=![]() �����ABD=60�㣬��BC=a����CN=
�����ABD=60�㣬��BC=a����CN=![]() a����Rt��PFN�У���PNF=��BNC=30�㣬��tan��PNF=
a����Rt��PFN�У���PNF=��BNC=30�㣬��tan��PNF=![]() ����FN=
����FN=![]() PF����MN=MF+FN=
PF����MN=MF+FN=![]() PF����S��BCN=2S��PMN����
PF����S��BCN=2S��PMN����![]() ����a=
����a=![]() PF����NC=
PF����NC=![]() a=
a=![]() PF����
PF����![]() =
=![]() =
=![]() ����MN=
����MN=![]() NC=
NC=![]() =
=![]() a����MC=MN+NC=��
a����MC=MN+NC=��![]() ��a����M��������4��a����
��a����M������Ϊ��4��a����![]() ��a������M�����������ϣ�����ɵ�
��a������M�����������ϣ�����ɵ�![]() =��
=��![]() ��a�����a=
��a�����a=![]() ��a=0����ȥ����OC=4��a=
��a=0����ȥ����OC=4��a=![]() ��MC=
��MC=![]() �����M��������
�����M��������![]() ��
��![]() ����
����

 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�