题目内容
若两个正数的算术平均数(即两数和的一半)为 ,几何平均数(即两数积的算术平方根)为
,几何平均数(即两数积的算术平方根)为 ,则这两个数的差是
,则这两个数的差是
- A.±6
- B.6
- C.±36
- D.36
A
分析:首先设出这两个数,然后根据这两个正数的算术平均数为 ,几何平均数为
,几何平均数为 ,列出等式求出这两个数的和及及积,最后利用完全平方式求解即可.
,列出等式求出这两个数的和及及积,最后利用完全平方式求解即可.
解答:设这两个数分别为a和b,
则根据题意得: =2
=2 ①,
①, =
= ②,
②,
①②两式联立解得:a2+b2=(a+b)2-2ab=48-6=42,
∴(a-b)2=a2+b2-2ab=42-2×3=36,
∴a-b=±6.
故选A.
点评:本题考查算术平方根和完全平方式的知识,解答该类题目的一般思路是分别求出这两个数,但此题行不通,注意整体思想的灵活运用.
分析:首先设出这两个数,然后根据这两个正数的算术平均数为
 ,几何平均数为
,几何平均数为 ,列出等式求出这两个数的和及及积,最后利用完全平方式求解即可.
,列出等式求出这两个数的和及及积,最后利用完全平方式求解即可.解答:设这两个数分别为a和b,
则根据题意得:
 =2
=2 ①,
①, =
= ②,
②,①②两式联立解得:a2+b2=(a+b)2-2ab=48-6=42,
∴(a-b)2=a2+b2-2ab=42-2×3=36,
∴a-b=±6.
故选A.
点评:本题考查算术平方根和完全平方式的知识,解答该类题目的一般思路是分别求出这两个数,但此题行不通,注意整体思想的灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
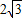 ,几何平均数(即两数积的算术平方根)为
,几何平均数(即两数积的算术平方根)为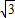 ,则这两个数的差是( )
,则这两个数的差是( )