题目内容
【题目】如图，在锐角三角形中，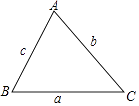 
（1）猜想 
， 
， 
之间的关系，并证明．
（2）猜想cosC与a，b，c之间的关系？并证明．
【答案】
（1）解： 
= 
= 
，
如图，作AD⊥BC于点D，作BE⊥AC于点E，
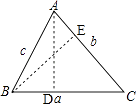
∴∠ADB=∠ADC=90°，
∴AD=ABsinB=ACsinC，即csinB=bsinC，
则 = ，
同理可得BE=csinA=asinC，即 = ，
∴ = =
（2）解：∵在Rt△ACD中，CD=ACcosC=bcosC，
∴BD=BC﹣CD=a﹣bcosC，
∵AB2﹣BD2=AC2﹣CD2，
∴c2﹣（a﹣bcosC）2=b2﹣（bcosC）2，
整理得cosC= 
【解析】（1）作AD⊥BC、作BE⊥AC，由AD=ABsinB=ACsinC，即csinB=bsinC得 = ，同理可得 = ，继而可得 = = ；（2）由CD=ACcosC=bcosC知BD=BC﹣CD=a﹣bcosC，根据AB2﹣BD2=AC2﹣CD2得c2﹣（a﹣bcosC）2=b2﹣（bcosC）2 ， 整理得cosC= ．
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．
【题目】学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数与碟子的高度的关系如下表：
碟子的个数 | 碟子的高度（单位：cm） |
1 | 2 |
2 | 2+1.5 |
3 | 2+3 |
4 | 2+4.5 |
… | … |
（1）当桌子上放有x（个）碟子时，请写出此时碟子的高度（用含x的式子表示）；
（2）分别从三个方向上看，其三视图如上图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度．
