题目内容
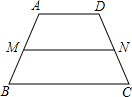 已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是
已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是
- A.22
- B.20
- C.18
- D.14
B
分析:此题只需根据“梯形的中位线等于两底和的一半”,求得梯形的两底和,再进一步计算其周长.
解答:∵MN是梯形ABCD的中位线,且MN=6,
∴AD+BC=2MN=2×6=12.
∴梯形ABCD的周长是AB+DC+AD+BD=4+4+12=20.
故选B.
点评:根据梯形中位线的性质和梯形的周长公式,解答即可.
分析:此题只需根据“梯形的中位线等于两底和的一半”,求得梯形的两底和,再进一步计算其周长.
解答:∵MN是梯形ABCD的中位线,且MN=6,
∴AD+BC=2MN=2×6=12.
∴梯形ABCD的周长是AB+DC+AD+BD=4+4+12=20.
故选B.
点评:根据梯形中位线的性质和梯形的周长公式,解答即可.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
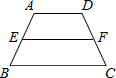 已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是( )
已知:在等腰梯形ABCD中,AD∥BC,AB=CD=5,EF是梯形ABCD的中位线,且EF=6,则梯形ABCD的周长是( )| A、24 | B、22 | C、20 | D、16 |
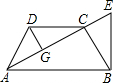 如图,已知:在等腰梯形ABCD中,AB∥CD,AC⊥BC,DG⊥AC,过B作EB⊥AB,交AC的延长线于E.
如图,已知:在等腰梯形ABCD中,AB∥CD,AC⊥BC,DG⊥AC,过B作EB⊥AB,交AC的延长线于E.
 4、已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是( )
4、已知:在等腰梯形ABCD中,AD∥BC,AB=CD=4,MN是梯形ABCD的中位线,且MN=6,则梯形ABCD的周长是( ) (2009•雅安)已知,在等腰梯形ABCD中,AD∥BC,AD=AB=2,∠B=60°,则梯形ABCD的周长( )
(2009•雅安)已知,在等腰梯形ABCD中,AD∥BC,AD=AB=2,∠B=60°,则梯形ABCD的周长( )