��Ŀ����
��ͼ1����������ABCD�У�AD��BC��AB=CD=| 10 |
��1���������ߵĺ�������ʽ��
��2���裨1���е���������BC���ڵ�E��P�Ǹ������߶Գ����ϵ�һ�����㣨��ͼ2����
����ֱ��PC���ı���AOEB������ֳ���ȵ������֣���ֱ��PC�ĺ�������ʽ��
������PB��PA���Ƿ���ڡ�PAB��ֱ�������Σ������ڣ�������з��������ĵ�P�����꣬��ֱ��д����Ӧ�ġ�PAB�����Բ��������������ڣ���˵�����ɣ�
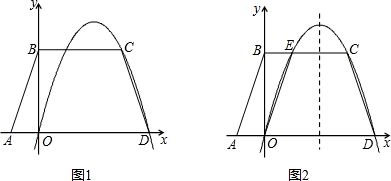
��������1�����ȹ���C��CF��AD��F����������ɵ�Rt��AOB��Rt��CFD����ɵ�C��3��3����D��4��0���������ô���ϵ����������ô������ߵĽ���ʽ��
��2��������AE��OB�ڵ�G����ΪE��������Ϊ3�����뼴�������������ֵ��������BE�ij������֤���ı���AOEB��ƽ���ı��Σ���PC����Gʱ��PC���ı���AOEB�����ƽ�֣��ɵ�C��G�����꣬���ô���ϵ�����������ֱ��PC�Ľ���ʽ��
���������M��N�����꣬�ٷֱ��PB2=PM2+BM2=��y-3��2+4��PA2=PM2+AM2=y2+9��AB2=10��������ȥ������ע�ⲻҪ©�⣬
��2��������AE��OB�ڵ�G����ΪE��������Ϊ3�����뼴�������������ֵ��������BE�ij������֤���ı���AOEB��ƽ���ı��Σ���PC����Gʱ��PC���ı���AOEB�����ƽ�֣��ɵ�C��G�����꣬���ô���ϵ�����������ֱ��PC�Ľ���ʽ��
���������M��N�����꣬�ٷֱ��PB2=PM2+BM2=��y-3��2+4��PA2=PM2+AM2=y2+9��AB2=10��������ȥ������ע�ⲻҪ©�⣬
��� �⣺��1������C��CF��AD��F��
�⣺��1������C��CF��AD��F��
����֪�ã�Rt��AOB��Rt��CFD��OF=BC=3��
��AO=DF=1��OD=OF+DF=4��
��CF=
=3��
��C��3��3����D��4��0����
��
��
��ã�a=-1��b=4��c=0��
�������������Ϊy=-x2+4x��
��2��������AE��OB�ڵ�G��
��y=3����y=-x2+4x��
�ã�-x2+4x=3��
��ã�x1=1��x2=3��
��E��1��3����
��BE=1=OA��
��BE��OA��
���ı���AOEB��ƽ���ı��Σ�
�൱PC����G��GΪAOEB�����Խ��ߵĽ��㣩ʱ��PC���ı���AOEB�����ƽ�֣�
��OG=
OB=
��
��G��0��
����
��C��3��3����
��ֱ��CGΪ��y=
x+
��
�༴ֱ��PCΪ��y=
x+
��
�ڴ������������ĵ�P��
�ɣ�1��֪�����ߵĶԳ���Ϊx=2��
��P��2��y�����Գ��ύBC�ڵ�M����x���ڵ�N��
��M��2��3����N��2��0����
��PB2=PM2+BM2=��y-3��2+4��PA2=PM2+AM2=y2+9��AB2=10��
�����ֿ��ܣ�
����PBA=90�㣬��PA2=PB2+AB2��
��y2+9=��y-3��2+4+10��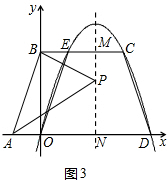
���y=
��
��P��2��
����
��AP=
=
��
��ʱ��PAB���Բ������ǣ��С���
��
��2=
�У�
����PAB=90�㣬��PB2=PA2+AB2��
�ࣨy-3��2+4=y2+9+10��
��ã�y=-1��
��P��2��-1����
��BP=2
��
��ʱ��PAB���Բ������ǣ�5�У�
����APB=90�㣬��PB2+PA2=AB2��
�ࣨy-3��2+4+y2+9=10���˷�����ʵ������
���ʱ���������ĵ�P�����ڣ�
�����������������������ĵ�P��
����P��2��
��ʱ����PAB���Բ�������
�У�
����P��2��-1��ʱ����PAB���Բ�������5�У�
 �⣺��1������C��CF��AD��F��
�⣺��1������C��CF��AD��F������֪�ã�Rt��AOB��Rt��CFD��OF=BC=3��
��AO=DF=1��OD=OF+DF=4��
��CF=
| CD2-DF2 |
��C��3��3����D��4��0����
��
|
��ã�a=-1��b=4��c=0��
�������������Ϊy=-x2+4x��
��2��������AE��OB�ڵ�G��
��y=3����y=-x2+4x��
�ã�-x2+4x=3��
��ã�x1=1��x2=3��
��E��1��3����
��BE=1=OA��
��BE��OA��
���ı���AOEB��ƽ���ı��Σ�
�൱PC����G��GΪAOEB�����Խ��ߵĽ��㣩ʱ��PC���ı���AOEB�����ƽ�֣�
��OG=
| 1 |
| 2 |
| 3 |
| 2 |
��G��0��
| 3 |
| 2 |
��C��3��3����
��ֱ��CGΪ��y=
| 1 |
| 2 |
| 3 |
| 2 |
�༴ֱ��PCΪ��y=
| 1 |
| 2 |
| 3 |
| 2 |
�ڴ������������ĵ�P��
�ɣ�1��֪�����ߵĶԳ���Ϊx=2��
��P��2��y�����Գ��ύBC�ڵ�M����x���ڵ�N��
��M��2��3����N��2��0����
��PB2=PM2+BM2=��y-3��2+4��PA2=PM2+AM2=y2+9��AB2=10��
�����ֿ��ܣ�
����PBA=90�㣬��PA2=PB2+AB2��
��y2+9=��y-3��2+4+10��

���y=
| 7 |
| 3 |
��P��2��
| 7 |
| 3 |
��AP=
(-1-2)2+(0-
|
| ||
| 3 |
��ʱ��PAB���Բ������ǣ��С���
| 1 |
| 2 |
| ||
| 3 |
| 65 |
| 18 |
����PAB=90�㣬��PB2=PA2+AB2��
�ࣨy-3��2+4=y2+9+10��
��ã�y=-1��
��P��2��-1����
��BP=2
| 5 |
��ʱ��PAB���Բ������ǣ�5�У�
����APB=90�㣬��PB2+PA2=AB2��
�ࣨy-3��2+4+y2+9=10���˷�����ʵ������
���ʱ���������ĵ�P�����ڣ�
�����������������������ĵ�P��
����P��2��
| 7 |
| 3 |
| 65 |
| 18 |
����P��2��-1��ʱ����PAB���Բ�������5�У�
���������⿼���˴���ϵ���������Ľ���ʽ���Լ�ƽ���ı��ε��ж������ʵ�֪ʶ�������ۺ��Ժ�ǿ��ע�����ν��˼�����������˼���Ӧ�ã�

��ϰ��ϵ�д�
 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
�����Ŀ
 1����ͼ���ڵ�������ABCD�У�AD��BC����B=60�㣬AD=AB����E��F�ֱ���AD��AB�ϣ�AE=BF��DF��CE�ཻ��P�����DPE=
1����ͼ���ڵ�������ABCD�У�AD��BC����B=60�㣬AD=AB����E��F�ֱ���AD��AB�ϣ�AE=BF��DF��CE�ཻ��P�����DPE= ��2005•բ������ģ����֪����ͼ���ڵ�������ABCD�У�AD��BC��AB=DC������D��AC��ƽ����DE����BA���ӳ����ڵ�E����֤��
��2005•բ������ģ����֪����ͼ���ڵ�������ABCD�У�AD��BC��AB=DC������D��AC��ƽ����DE����BA���ӳ����ڵ�E����֤�� ��2013•�Ϻӿ���ģ�⣩��ͼ���ڵ�������ABCD�У�AD��BC��AB=AD��BC=��
��2013•�Ϻӿ���ģ�⣩��ͼ���ڵ�������ABCD�У�AD��BC��AB=AD��BC=�� ���У���һ�����˶����յ�ʱ�������˶�����ֹ������P��Qͬʱ�������˶���t�룺
���У���һ�����˶����յ�ʱ�������˶�����ֹ������P��Qͬʱ�������˶���t�룺 ����
����