题目内容
 (2013•老河口市模拟)如图,在等腰梯形ABCD中,AD∥BC,AB=AD,BC=(
(2013•老河口市模拟)如图,在等腰梯形ABCD中,AD∥BC,AB=AD,BC=(| 2 |
75°或165°
75°或165°
.分析:过点A作AF∥CD交BC于F,可得四边形AFCD是平行四边形,根据平行四边形的对边相等可得AD=FC,AF=CD,再求出BF,然后利用勾股定理逆定理判定△ABF是等腰直角三角形,根据等腰直角三角形的性质求出∠ABF=45°,根据两直线平行,同旁内角互补求出∠BAD=135°,然后分①点E在AD的上方时,根据周角等于360°求出∠BAE,根据等腰三角形两底角相等求出∠ABE,然后根据三角形的内角和定理列式计算即可得解;②点E在AD的下方时,求出∠BAE,再根据等腰三角形两底角相等求出∠ABE,然后求出∠CBE,再利用三角形的内角和定理列式计算即可得解.
解答:解:在等腰梯形ABCD中,AB=CD,
过点A作AF∥CD交BC于F,
∵AD∥BC,
∴四边形AFCD是平行四边形,
∴AD=FC,AF=CD,
∵AB=AD,BC=(
+1)AD,
∴BF=BC-FC=(
+1)AD-AD=
AD,
在△ABF中,AB2+AF2=AD2+AD2=2AD2=BF2,
∴△ABF是等腰直角三角形,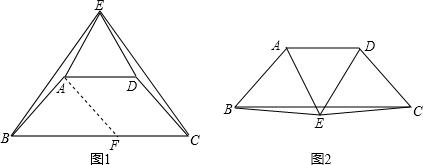
∴∠ABF=45°,
∵AD∥BC,
∴∠BAD=180°-∠ABF=180°-45°=135°,
①如图1,等边三角形ADE的顶点E在AD的上方时,
∠BAE=360°-60°-135°=165°,
∵AB=AD=AE,
∴∠ABE=
(180°-165°)=7.5°,
∴∠CBE=∠ABF+∠ABE=45°+7.5°=52.5°,
同理可得∠BCE=52.5°,
∴∠BEC=180°-52.5°×2=75°;
②如图2,等边三角形ADE的顶点E在AD的下方时,
∠BAE=∠BAD-∠DAE=135°-60°=75°,
∵AB=AD=AE,
∴∠ABE=
(180°-75°)=52.5°,
∴∠CBE=∠ABE-∠ABC=52.5°-45°=7.5°,
同理可得∠BCE=7.5°,
∴∠BEC=180°-7.5°×2=165°;
综上所述,∠BEC=75°或165°.
故答案为:75°或165°.
过点A作AF∥CD交BC于F,
∵AD∥BC,
∴四边形AFCD是平行四边形,
∴AD=FC,AF=CD,
∵AB=AD,BC=(
| 2 |
∴BF=BC-FC=(
| 2 |
| 2 |
在△ABF中,AB2+AF2=AD2+AD2=2AD2=BF2,
∴△ABF是等腰直角三角形,

∴∠ABF=45°,
∵AD∥BC,
∴∠BAD=180°-∠ABF=180°-45°=135°,
①如图1,等边三角形ADE的顶点E在AD的上方时,
∠BAE=360°-60°-135°=165°,
∵AB=AD=AE,
∴∠ABE=
| 1 |
| 2 |
∴∠CBE=∠ABF+∠ABE=45°+7.5°=52.5°,
同理可得∠BCE=52.5°,
∴∠BEC=180°-52.5°×2=75°;
②如图2,等边三角形ADE的顶点E在AD的下方时,
∠BAE=∠BAD-∠DAE=135°-60°=75°,
∵AB=AD=AE,
∴∠ABE=
| 1 |
| 2 |
∴∠CBE=∠ABE-∠ABC=52.5°-45°=7.5°,
同理可得∠BCE=7.5°,
∴∠BEC=180°-7.5°×2=165°;
综上所述,∠BEC=75°或165°.
故答案为:75°或165°.
点评:本题考查了等腰梯形的性质,等边三角形的性质,勾股定理逆定理的应用,等边对等角的性质,梯形的问题关键在于作辅助线,本题利用勾股定理逆定理判断出△ABF是等腰直角三角形是解题的关键,难点在于要分情况讨论.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 (2013•老河口市模拟)如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=15°,则∠2的余角的度数是( )
(2013•老河口市模拟)如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=15°,则∠2的余角的度数是( )