题目内容
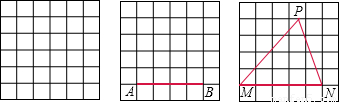
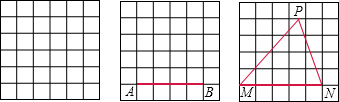
如果正方形网格中的每一个小正方形边长都是1,则每个小格的顶点叫做格点.(1)在图a中以格点为顶点画一个三角形,使三角形的三边长分别为3、
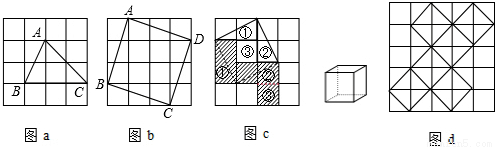
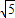 、2
、2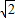 ;
;(2)在图b中以格点为顶点画一个面积为10的正方形;
(3)观察图c中带阴影的图形,请你将它适当剪开,重新拼成一个正方形;(要求:在图c中用虚线作出,并用文字说明剪拼方法)图c说明:______.
(4)观察正方体,沿着一些棱将它剪开,展开成平面图形.若正方体的表面积为12,请你在图d中以格点为顶点画出一个正方体的平面展开图.(只需画出一种情形)
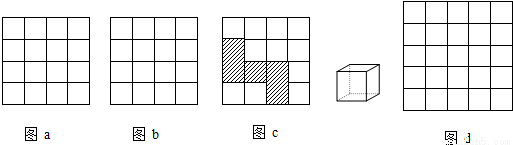
【答案】分析:(1)根据网格结构,利用勾股定理作出相邻两格的对角线为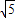 ,2格的正方形的对角线为2
,2格的正方形的对角线为2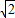 ,然后再以边长为3格三条线段为边长作出三角形即可;
,然后再以边长为3格三条线段为边长作出三角形即可;
(2)以相邻3格的对角线为边长作出正方形即为所求作的正方形;
(3)阴影部分共有5个小正方形,面积为5,所以作出的正方形的边长为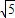 ,然后沿相邻2个正方形的对角线剪开即可,再进行拼接即可;
,然后沿相邻2个正方形的对角线剪开即可,再进行拼接即可;
(4)根据正方体的表面积可以求出正方体的棱长为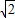 ,然后根据网格结构作出边长为
,然后根据网格结构作出边长为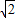 的“1、4、1”结构的一个正方体展开图即可.
的“1、4、1”结构的一个正方体展开图即可.
解答:解:(1)如图所示,△ABC即为所求作的三角形;
(2)如图所示,正方形ABCD的面积为10;
(3)如图所示,沿虚线剪开,然后①、②、③分别对应拼接即可得解;
(4)∵正方体有6个表面,
∴每一个面的表面积为12÷6=2,
所以,正方体的棱长为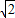 ,
,
如图所示,为正方体的一种平面展开图.
点评:本题考查了应用与设计作图,熟练掌握网格结构的特点,勾股定理,正方形的性质,正方体的常见的平面展开图的形式是解题的关键,本题综合性较强,有难度.
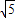 ,2格的正方形的对角线为2
,2格的正方形的对角线为2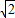 ,然后再以边长为3格三条线段为边长作出三角形即可;
,然后再以边长为3格三条线段为边长作出三角形即可;(2)以相邻3格的对角线为边长作出正方形即为所求作的正方形;
(3)阴影部分共有5个小正方形,面积为5,所以作出的正方形的边长为
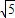 ,然后沿相邻2个正方形的对角线剪开即可,再进行拼接即可;
,然后沿相邻2个正方形的对角线剪开即可,再进行拼接即可;(4)根据正方体的表面积可以求出正方体的棱长为
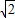 ,然后根据网格结构作出边长为
,然后根据网格结构作出边长为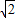 的“1、4、1”结构的一个正方体展开图即可.
的“1、4、1”结构的一个正方体展开图即可.解答:解:(1)如图所示,△ABC即为所求作的三角形;
(2)如图所示,正方形ABCD的面积为10;
(3)如图所示,沿虚线剪开,然后①、②、③分别对应拼接即可得解;
(4)∵正方体有6个表面,
∴每一个面的表面积为12÷6=2,
所以,正方体的棱长为
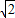 ,
,如图所示,为正方体的一种平面展开图.

点评:本题考查了应用与设计作图,熟练掌握网格结构的特点,勾股定理,正方形的性质,正方体的常见的平面展开图的形式是解题的关键,本题综合性较强,有难度.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目

 、2
、2 ;
;
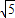 、2
、2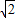 ;
;