题目内容
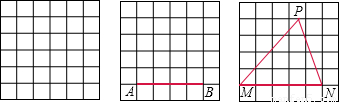
（2006•舟山）如果正方形网格中的每一个小正方形边长都是1，则每个小格的顶点叫做格点．（1）在图1中，以格点为顶点画一个三角形，使三角形的三边长分别为3、
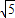、2
；（2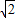）在图2中，线段AB的端点在格点上，请画出以AB为一边的三角形，使这个三角形的面积为6；（要求至少画出3个）；
（3）在图3中，△MNP的顶点M、N在格点上，P在小正方形的边上，问这个三角形的面积相当于多少个小方格的面积？在你解出答案后，说说你的解题方法．
【答案】分析：（1）可先画3的线段，根据勾股定理可得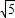
为长为2，宽为1的矩形的对角线，2
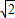是边长为2的正方形的对角线，作图即可；
（2）作高为3的三角形即可；
（3）相当于10个小方格的面积，作PA⊥MN于A，可得全等的两对三角形，在4×5的网格中，△MNP的面积是这些小格的一半，即相当于10个小方格的面积．
解答：解：（1）、（2）如图：
；
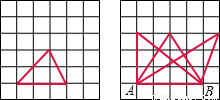（3）相当于10个小方格的面积，
作PA⊥MN于A，可得全等的两对三角形，即△PAM≌△MBP，△PAN≌△NCP，
那么在4×5的网格中，△MNP的面积是矩形MNCB的一半，即相当于10个小方格的面积．
点评：考查无理数概念、勾股定理的应用、三角形有关知识的综合运用．
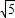为长为2，宽为1的矩形的对角线，2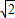是边长为2的正方形的对角线，作图即可；（2）作高为3的三角形即可；
（3）相当于10个小方格的面积，作PA⊥MN于A，可得全等的两对三角形，在4×5的网格中，△MNP的面积是这些小格的一半，即相当于10个小方格的面积．
解答：解：（1）、（2）如图：
；（3）相当于10个小方格的面积，
作PA⊥MN于A，可得全等的两对三角形，即△PAM≌△MBP，△PAN≌△NCP，
那么在4×5的网格中，△MNP的面积是矩形MNCB的一半，即相当于10个小方格的面积．
点评：考查无理数概念、勾股定理的应用、三角形有关知识的综合运用．
练习册系列答案
阅读快车系列答案
相关题目
