题目内容
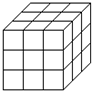一个正方体的表面涂满了颜色，按如图所示将它切成27个大小相等的小立方块，设其中仅有i个面（i=1，2，3）涂有颜色的小立方块的个数为xi，则x1，x2，x3之间的关系为（ ）分析：根据图示：在原正方体的8个顶点处的8个小正方体上，有3个面涂有颜色；2个面涂有颜色的小正方体有12个，1个面涂有颜色的小正方体有6个．
解答：解：根据以上分析可知x1+x3-x2=6+8-12=2．
故选D．
故选D．
点评：此题主要考查了立体图形的性质，根据已知得出涂有颜色不同的小立方体的个数是解题关键．
练习册系列答案
相关题目
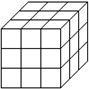5、一个正方体的表面涂满了颜色，按如图所示将它切成27个大小相等的小立方块，设其中仅有i个面（1，2，3）涂有颜色的小立方块的个数为xi，则x1、x2、x3之间的关系为（ ）
