题目内容
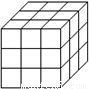
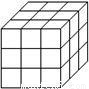
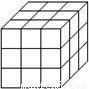
一个正方体的表面涂满了颜色，按如图所示将它切成27个大小相等的小立方块，设其中仅有i个面（1，2，3）涂有颜色的小立方块的个数为xi，则x1、x2、x3之间的关系为（ ）
A．x1-x2+x3=1
B．x1+x2-x3=1
C．x1+x3-x2=2
D．x1-x3+x2=2
【答案】分析：根据图示：在原正方体的8个顶点处的8个小正方体上，有3个面涂有颜色；2个面涂有颜色的小正方体有12个，1个面涂有颜色的小正方体有6个．
解答：解：根据以上分析可知x1+x3-x2=2．
故选C．
点评：认真仔细读题意，掌握图形的特点，及正方体共有8个顶点和6个面．
解答：解：根据以上分析可知x1+x3-x2=2．
故选C．
点评：认真仔细读题意，掌握图形的特点，及正方体共有8个顶点和6个面．
练习册系列答案
相关题目
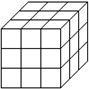5、一个正方体的表面涂满了颜色，按如图所示将它切成27个大小相等的小立方块，设其中仅有i个面（1，2，3）涂有颜色的小立方块的个数为xi，则x1、x2、x3之间的关系为（ ）
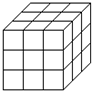一个正方体的表面涂满了颜色，按如图所示将它切成27个大小相等的小立方块，设其中仅有i个面（i=1，2，3）涂有颜色的小立方块的个数为xi，则x1，x2，x3之间的关系为（ ）
