题目内容
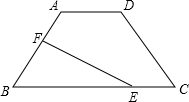 如图,在等腰梯形ABCD中,AB=DC=5,AD=4,BC=10,点E在下底边BC上,点F在腰AB上.
如图,在等腰梯形ABCD中,AB=DC=5,AD=4,BC=10,点E在下底边BC上,点F在腰AB上.(1)若EF平分等腰梯形ABCD的周长,设BE长为x,试用含x的代数式表示BF及△BEF
的面积(提示:作AK⊥BC于K,作FG⊥BC于G);
(2)是否存在线段EF将等腰梯形ABCD的周长和面积同时平分?若存在,求出此时BE的长;若不存在,请说明理由.
分析:(1)作AK⊥BC于K,FG⊥BC于G,根据△FBG∽△ABK对应边成比例即可求解;
(2)根据四边形的面积即可求出x的值.
(2)根据四边形的面积即可求出x的值.
解答: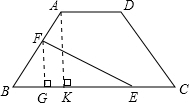 解:(1)梯形的周长为4+2×5+10=24,
解:(1)梯形的周长为4+2×5+10=24,
由题意:BF+EB=12,即BF+x=12,
∴BF=12-x,作AK⊥BC于K,FG⊥BC于G,
则BK=3,AK=4,
又∵△FBG∽△ABK,
∴
=
,即
=
,
∴FG=
(12-x),
∴△BEF的面积=
BE•FG=
(-x2+12x);
(2)又∵S四边形ABCD=
(10+4)×4=28,则
(-x2+12x)=14,
解得:x=5或x=7,
∵BF=12-x≤5,
∴x≥7,
∴x=7,
即存在线段EF将等腰梯形的周长和面积同时平分.
 解:(1)梯形的周长为4+2×5+10=24,
解:(1)梯形的周长为4+2×5+10=24,由题意:BF+EB=12,即BF+x=12,
∴BF=12-x,作AK⊥BC于K,FG⊥BC于G,
则BK=3,AK=4,
又∵△FBG∽△ABK,
∴
| FG |
| AK |
| FB |
| AB |
| GF |
| 4 |
| 12-x |
| 5 |
∴FG=
| 4 |
| 5 |
∴△BEF的面积=
| 1 |
| 2 |
| 2 |
| 5 |
(2)又∵S四边形ABCD=
| 1 |
| 2 |
| 2 |
| 5 |
解得:x=5或x=7,
∵BF=12-x≤5,
∴x≥7,
∴x=7,
即存在线段EF将等腰梯形的周长和面积同时平分.
点评:本题考查了相似三角形的判定与性质,难度适中,关键是巧妙地作出辅助线.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 在,求出这样的t的值;若不存在,请说明理由.
在,求出这样的t的值;若不存在,请说明理由. 10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE.
10、如图,在等腰梯形ABCD中,AD∥BC,AB=DC,E为AD的中点,求证:BE=CE. 已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD.
已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E、F分别在AB、DC上,且BE=3EA,CF=3FD. (2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
(2012•广州)如图,在等腰梯形ABCD中,BC∥AD,AD=5,DC=4,DE∥AB交BC于点E,且EC=3,则梯形ABCD的周长是( )
