��Ŀ����
����Ŀ����֪�����Ĺ�ϵʽ��L1��y=kx2+��k��2��x��2
��1������˵������ȷ������� ��
�ٵ�k=1ʱ���䶥������Ϊ��![]() ��
��![]() ����
����
�ڵ�k=2ʱ�����κ�����ͼ�����y��Գƣ�
������kΪ�η���ֵ�����κ�������������1��0���ͣ�0����2����
��2����֤������kΪ��ֵʱ������ͼ����x�����н��㣻
��3����֪���κ���L1��ͼ����x���ཻ�ڵ�A��B������ΪP����k��0������ABPΪ�ȱ������Σ���k��ֵ��
���𰸡���1���ڢۣ���2������������3��2![]() ��2��
��2��
��������
�����������1����k=1ʱ����y=x2��x��2��ɶ���ʽ���ɶԢٽ����жϣ���k=2ʱ��y=2x2��2�������ߵĶԳ���Ϊy�ᣬ��ɶԢڽ����жϣ����ݶ��κ���ͼ���ϵ�����������Ԣ۽����жϣ�
��2���������ۣ���k=0ʱ��ԭ����Ϊһ�κ���y=��2x��2����ͼ��һ����x����һ�����㣻��k��0ʱ�������б�ʽ��������ж϶��κ���ͼ����x���н��㣬��������kΪ��ֵʱ������ͼ����x�����н��㣻
��3��������������x��Ľ������⣬�ⷽ��kx2+��k��2��x��2=0�ɵ�A��![]() ��0����B����1��0��������P������Ϊ��
��0����B����1��0��������P�������� ![]() ����
����![]() ������k��0ʱ��AB=
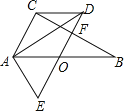
������k��0ʱ��AB=![]() ����ͼ1����DE��x����E�����ݵȱ������ε����ʵ�DE=
����ͼ1����DE��x����E�����ݵȱ������ε����ʵ�DE=![]() AB����
AB���� ![]() =
=![]() ��
��![]() �����k1=��2����ȥ����k2=2
�����k1=��2����ȥ����k2=2![]() ��2������k��ֵΪ2
��2������k��ֵΪ2![]() ��2��
��2��
��1���⣺��k=1ʱ��y=x2��x��2=��x��![]() ��2��
��2��![]() ����ʱ��������Ϊ��
����ʱ��������Ϊ��![]() ����
����![]() �������Ԣٴ���
�������Ԣٴ���
��k=2ʱ��y=2x2��2���������ߵĶԳ���Ϊy�ᣬ���Ԣ���ȷ��
��x=��1ʱ��y=kx2+��k��2��x��2=k��k+2��2=0����x=0ʱ��y=kx2+��k��2��x��2=��2����������kΪ�η���ֵ�����κ�������������1��0���ͣ�0����2�������Ԣ���ȷ��
�ʴ�Ϊ���ڢۣ�
��2��֤������k=0ʱ��һ�κ���y=��2x��2��x����һ�����㣨��1��0����
��k��0ʱ����=��k��2��2��4k����2��=��k+2��2��0���˶��κ���ͼ����x���н��㣬
��������kΪ��ֵʱ������ͼ����x�����н��㣻
��3���⣺��y=0ʱ��kx2+��k��2��x��2=0�����x1=��1��x2=![]() ��
��
��A��![]() ��0����B����1��0��������P��������
��0����B����1��0��������P��������![]() ����
����![]() ����
����
AB=![]() +1����ͼ1����DE��x����E��
+1����ͼ1����DE��x����E��
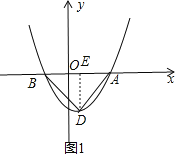
�ߡ�ABPΪ�ȱ������Σ�
��DE=![]() AB����
AB���� ![]() =
=![]() ��
��![]() ��
��
���k1=��2����ȥ����k2=2![]() ��2��
��2��
��k��ֵΪ2![]() ��2��
��2��

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�