题目内容
 如图,∠CBD、∠ABD为△ABD的两个外角,∠CBD=70°,∠ADE=149°,则∠A的度数是
如图,∠CBD、∠ABD为△ABD的两个外角,∠CBD=70°,∠ADE=149°,则∠A的度数是
- A.28°
- B.31°
- C.39°
- D.42°
C
分析:根据平角的定义求出∠ABD,根据三角形的外角性质得出∠ADE=∠ABD+∠A,代入即可求出答案.
解答:∵∠ABD+∠CBD=180°,∠CBD=70°,
∴∠ABD=110°,
∵∠ADE=∠ABD+∠A,∠ADE=149°,
∴∠A=39°.
故选C.
点评:本题主要考查对三角形的外角性质,邻补角的定义等知识点的理解和掌握,能灵活运用三角形的外角性质进行计算是解此题的关键.
分析:根据平角的定义求出∠ABD,根据三角形的外角性质得出∠ADE=∠ABD+∠A,代入即可求出答案.
解答:∵∠ABD+∠CBD=180°,∠CBD=70°,
∴∠ABD=110°,
∵∠ADE=∠ABD+∠A,∠ADE=149°,
∴∠A=39°.
故选C.
点评:本题主要考查对三角形的外角性质,邻补角的定义等知识点的理解和掌握,能灵活运用三角形的外角性质进行计算是解此题的关键.

练习册系列答案
相关题目
 3、如图,∠CBD、∠ABD为△ABD的两个外角,∠CBD=70°,∠ADE=149°,则∠A的度数是( )
3、如图,∠CBD、∠ABD为△ABD的两个外角,∠CBD=70°,∠ADE=149°,则∠A的度数是( )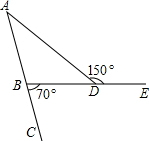 如图,∠CBD,∠ADE为△ABD的两个外角,∠CBD=70°,∠ADE=150°,则∠A的度数是( )
如图,∠CBD,∠ADE为△ABD的两个外角,∠CBD=70°,∠ADE=150°,则∠A的度数是( ) 如图,∠CBD,∠ADE为△ABD的两个外角,∠CBD=70°,∠ADE=150°,则∠A的度数是
如图,∠CBD,∠ADE为△ABD的两个外角,∠CBD=70°,∠ADE=150°,则∠A的度数是