题目内容
如图,在平面直角坐标系xOy中,直线 与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处
与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处
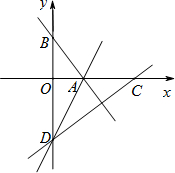
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式
 与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处
与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处 
(1)求AB的长和点C的坐标;
(2)求直线CD的解析式
(1)10,(16,0) (2)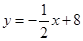
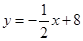
试题分析:(1)在平面直角坐标系xOy中,直线
 与x轴,y轴分别交于点A,点B,当x=0时, y=
与x轴,y轴分别交于点A,点B,当x=0时, y=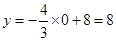 ,所以B点的坐标为(0,8),所以OA=8,当y=0,则
,所以B点的坐标为(0,8),所以OA=8,当y=0,则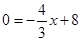 ,解得x=6,那么A点的坐标为(6,0),所以OB=6,因此AB的长=
,解得x=6,那么A点的坐标为(6,0),所以OB=6,因此AB的长=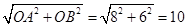 ;若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处,点B的坐标为(0,8),根据折叠的特征AB=AC,所以OC=OA+AC=6+10=16,所以点C的坐标为(16,0)
;若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处,点B的坐标为(0,8),根据折叠的特征AB=AC,所以OC=OA+AC=6+10=16,所以点C的坐标为(16,0)(2)点D在y轴的负半轴上,由(1)知B点的坐标为(0,8),所以点D的坐标为(0,-8),由(1)知点C的坐标为(16,0),因为直线CD过点C、D,所以设直线CD的解析式为y=kx+b,则
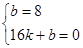 ,解得
,解得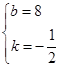 ,所以直线CD的解析式
,所以直线CD的解析式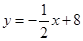
点评:本题考查一次函数,勾股定理,折叠,解答本题需要掌握用待定系数法求一次函数的解析式,熟悉勾股定理的内容,熟悉折叠的性质

练习册系列答案
相关题目
 中,自变量x的取值范围是
中,自变量x的取值范围是 中自变量
中自变量 的取值范围是 .
的取值范围是 .
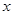 轴的负方向平移6个单位,它与点 重合。
轴的负方向平移6个单位,它与点 重合。 轴是什么关系?
轴是什么关系? ,则点A(
,则点A( ,
, ) ( )
) ( ) 中自变量x的取值范围是 .
中自变量x的取值范围是 . 是
是 的函数的是
的函数的是